- #1
FredericChopin
- 101
- 0
Hello,
I have been doing a review test on Geometry 1 on Sparknotes (http://www.sparknotes.com/math/geometry1/review/quiz.html), however I came across two questions which I got incorrect answers for and which I found the provided solutions questionable.
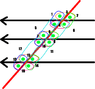
The first is Question 1 (attached).
I managed to find only 16 pairs of angles which were supplementary (attached is my solution), however this is not one of the solutions presented and the correct answer was that there were 36 pairs of supplementary angles.
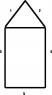
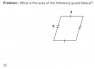
The second is Question 2 (attached).
Simply attaching a triangle on a quadrilateral yields a pentagon, but in no way does it ever yield a quadrilateral, which was the correct solution to Question 2.
If you could suggest where I must have gone wrong, that would be appreciated.
Thank you.
I have been doing a review test on Geometry 1 on Sparknotes (http://www.sparknotes.com/math/geometry1/review/quiz.html), however I came across two questions which I got incorrect answers for and which I found the provided solutions questionable.
The first is Question 1 (attached).
I managed to find only 16 pairs of angles which were supplementary (attached is my solution), however this is not one of the solutions presented and the correct answer was that there were 36 pairs of supplementary angles.
The second is Question 2 (attached).
Simply attaching a triangle on a quadrilateral yields a pentagon, but in no way does it ever yield a quadrilateral, which was the correct solution to Question 2.
If you could suggest where I must have gone wrong, that would be appreciated.
Thank you.