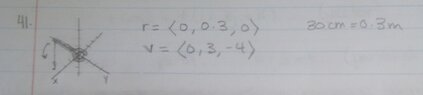ineedhelpnow
- 649
- 0
HEY GUYS! (Wave)
ok so i have this question i did. and now I am reviewing for the test and i looked at how i did it and i did in the most complicated way ever. i don't FULLY understand chegg's method. so i hope someone can provide me with the SIMPLEST method possible. thank u! (Blush) (p.s. don't ask me what the green stain on my final answer is because i have no idea) i would really appreciate a step by step solution at one shot so i can fully understand it.
View attachment 3211View attachment 3213View attachment 3212View attachment 3210
$\left| \tau\right| = \left| r \right| \left| F \right| sin (\theta)$
ok so i have this question i did. and now I am reviewing for the test and i looked at how i did it and i did in the most complicated way ever. i don't FULLY understand chegg's method. so i hope someone can provide me with the SIMPLEST method possible. thank u! (Blush) (p.s. don't ask me what the green stain on my final answer is because i have no idea) i would really appreciate a step by step solution at one shot so i can fully understand it.
View attachment 3211View attachment 3213View attachment 3212View attachment 3210
$\left| \tau\right| = \left| r \right| \left| F \right| sin (\theta)$