MHB Revolving Volume of R on x=3 using Shell Method

[jaychay]

If the area of R is equal to 2 m^2 and the volume of R is equal to 4pi m^3 when it's revolving on Y by using shell method. Find the volume of R when it's revolving on x=3 ?

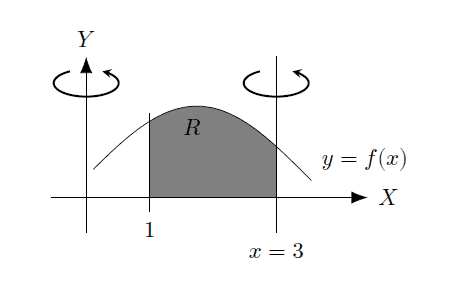
Can you please help me ?
I have tried to do it many times but still got the wrong answer.
Thank you in advance.

 

[skeeter]

$\displaystyle R = \int_1^3 f(x) \, dx = 2m^2$

$\displaystyle V_{x=0} = 2\pi \int_1^3 x \cdot f(x) \, dx = 4\pi m^3$

$\displaystyle V_{x=3} = 2\pi \int_1^3 (3-x) \cdot f(x) \, dx = \, ?$

 

[jaychay]

$\displaystyle R = \int_1^3 f(x) \, dx = 2m^2$

$\displaystyle V_{x=0} = 2\pi \int_1^3 x \cdot f(x) \, dx = 4\pi m^3$

$\displaystyle V_{x=3} = 2\pi \int_1^3 (3-x) \cdot f(x) \, dx = \, ?$

Thank you very much.
I finally find the answer.