Lynch101
Gold Member
- 772
- 85
- TL;DR Summary
- Based on feedback, I want to attempt a more rigorous argument about the 'location' of the QM system prior to measurement.
In the other thread of a similar name it was stated, and probably rightly so, that I wasn't using rigorous terminology or that I wasn't using them in a rigorous way. While I was making certain assumptions about the ability to interpret the 'jargon' I was using, it seemed to be a serious impediment to interpreting the argument that was being put forward. For that reason, I am going to attempt to define or describe the terms I am using with a bit more rigour, in the hope that that argument I am putting forward will be more intelligible. This will either highlight the error in my reasoning or, with an infinitesimal probability, prove to be a convincing argument.
This is strictly meant as an argument against the completeness of any interpretation in which the mathematics only predicts the measurement outcomes of an ensemble of similarly prepared systems.
I would ask that people apply the principles of 'steelman' (the opposite of 'strawman').The Physical Set-up
We can apply the reasoning to several different set-ups but I will have both the Stern-Gerlach and double-slit experiments in mind. I will attempt to make it clear where I am talking about one or the other.
So, in the laboratory, we have the experimental set-up like such:
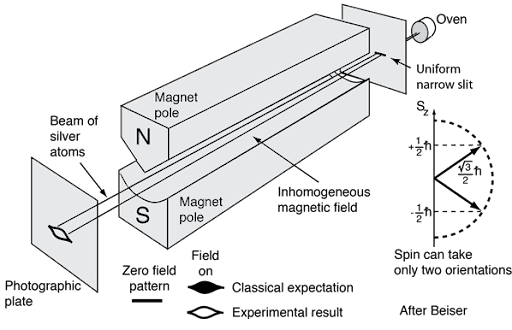
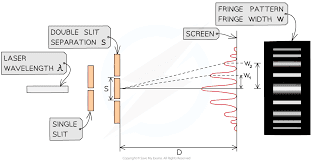
These are graphical representations of real-world experimental set-ups. The equipment in the lab, the lab, and the universe are what we refer to as 'the real world' or 'the physical world'. This is contrasted with the the mathematical/graphical representation of the experimental set-up.
In the reference frame of any given user, the physical world is observed to be 3 Dimensional.
The Mathematical/Graphical Representation
We can represent the 3D world mathematically and graphically by using a co-ordinate reference system, where the three dimensions of space are represented using X, Y, and Z axes. These axes can be extended indefinitely in each direction to allow us to represent the entire 3D universe or, at least, enough of the 3D universe as we need for this argument. Using this co-ordinate system, the lab equipment and everything else in the 3D universe can be represented.Location Within Finite Regions of Space
For simplicity sake, we can imagine that there is a wooden box in the laboratory. Inside this box there is space enough for us to place an array of different items. The space inside this box, as enclosed by the boundaries/sides of the box, is a finite 'region of space'.
We can also represent the box mathematically/graphically along with the finite region of space it encloses. We can do this by drawing a cuboid with the corresponding measurements and shading the area inside the cuboid i.e. inside the lines which represent the sides. The shaded area represent the finite region of space, inside the box.
As we mentioned, we can place an array of objects (or systems) inside the box. Something is said to be 'located within the finite region of space [of the box]' if it is anywhere within the shaded area i.e. anywhere inside the box. To illustrate this point, we could place a pregnant cat inside the box and close the lid. Now, we might not be able to represent then exact position of the cat inside the box, but we can say that the cat is, most certainly, 'located within the finite region of space of the box'.
Quantum experiments are somewhat different from putting cats in boxes although thought experiments with cats in boxes can provide useful analogies.
Quantum Experiments
With our experimental set-ups we have a piece of equipment which prepares the quantum system and at some later time, t, we have a measurement outcome on a screen.
One of our assumptions is that the preparation equipment can only exert a causal influence which propagates through 3D space at a maximum speed c i.e. the speed of light and that any system created by the preparation device can travel no faster than c. If this is the case, then that allows us to define a finite region/volume of 3D space* within which the system prepared by the device must be located. If it were possible to measure the system outside this finite region of space i.e. if there were a non-zero probability of measuring it outside this region, that would necessitate that the system had traveled FTL or that it does not operate in 3D space.
*a sphere with radius ct.
Possible Paths
There are an infinite number of possible paths from the preparation device to the measured outcome and we could, theoretically, represent those infinite number of possible paths, graphically. Some of those would all fall within our sphere of radius ct. Those that fall within the sphere represent the possible paths a system limited to the speed of light could take.
Intuitively, we might think of the paths taken being those of a point particle [with a definite position and momentum], but we can't necessarily do that for quantum systems. Instead, what we can say is that whatever path the system took, from preparation device to measured position, it must have been within the finite region of space enclosed by the sphere with radius ct.
To say that something 'passes through' the finite region of space we simply mean:
1) it took one of the possible paths within the finite region of space enclosed by the sphere
2) it took every possible path within the finite region of space enclosed by the sphere
3) it too more than one possible path within the finite region of space enclosed by the sphere.
If the possible paths of the system from preparation device to measured position must fall within the sphere of radius ct, then we can say with certainty, that the system was located within the finite region of space i.e. that its position was somewhere within that finite region of space. Where position doesn't have to take a single, pre-defined value.
In the case of the Stern-Gerlach experiement, we can set-up two SG magnets (A and B) and two detector screens. But we need use only one preparation device. We can define (and graphically represent) the finite regions of space occupied by the different magentic fields. If we can say the system 'passes through' the region of space occupied by magetic field A but doesn't 'pass through' the adjacent magnetic field B, then we can narrow down the position/location of the system to the finite region of space occupied by magnet A.
Probability of Position
There is a difference between the following statements:
1) There is a non-zero probability of measuring the system in position X.
2) The system is in position X with a probability of 1 or 0.
As mentioned, we can [in principle] represent all possible paths the system could have taken from preparation device to measured outcome. These don't have to be the paths of a point particle with definite position and momentum. There are possibly an infinite number of such paths, but the probability that the system took each path is either 1 or 0 i.e. it either took Path 1, or it didn't; it either took path 2 or it didn't. This is true if the system operates in 3 dimensional space.
This means that prior to measurement, for any possible position within the finite region of space, the system is in that position with a probability of 1 or 0. It is not necessary that the system be in a single, pre-defined positon and that single, pre-defined position only, since it is possible for it to be in multiple positons with a probability of 1.
This is a separate proposition to the probability that when we measure the system it will always be in a single, well-defined position. However, if a system is always in a given positon with a probability of 1 or 0, and cannot be only one single position with a probability of 1, it must be in multiple positions simultaneously. If we always measure it in only one well-defined position then there must be some sort of physical, FTL collapse of the system.
Alternatively, the system does not operate in 3 dimensions.Schroedingers Kittens
To use an analogy. Imagine that we have never witnessed kittens being born before. For some reason, the birthing process only ever seems to occur when we we put a kitten preparation device (i.e. a cat) into a closed, finite region of space e.g. a closed box. We have an intuitive idea about how the birthing process works but our calculations tell us that cats giving birth to kittens don't behave the same way that other animals do.
So, we put the pregnant cat in the box and we know that at some time t when we open the box, we will find a single kitten in a well defined position inside the box. But, prior to opening the box we don't know what the position of the kitten is. However, we know for absolute certain that it must have some position inside the box. The probability of the position of the kitten in the box cannot be 0 everywhere in the box, it must be 1 in at least one position.
Our calculations tell us that it cannot be 1 in just one position, so therefore, it must be 1 in multiple positons. Otherwise, the birthing process does not occur in only 3 dimensions.
This is strictly meant as an argument against the completeness of any interpretation in which the mathematics only predicts the measurement outcomes of an ensemble of similarly prepared systems.
I would ask that people apply the principles of 'steelman' (the opposite of 'strawman').The Physical Set-up
We can apply the reasoning to several different set-ups but I will have both the Stern-Gerlach and double-slit experiments in mind. I will attempt to make it clear where I am talking about one or the other.
So, in the laboratory, we have the experimental set-up like such:
These are graphical representations of real-world experimental set-ups. The equipment in the lab, the lab, and the universe are what we refer to as 'the real world' or 'the physical world'. This is contrasted with the the mathematical/graphical representation of the experimental set-up.
In the reference frame of any given user, the physical world is observed to be 3 Dimensional.
The Mathematical/Graphical Representation
We can represent the 3D world mathematically and graphically by using a co-ordinate reference system, where the three dimensions of space are represented using X, Y, and Z axes. These axes can be extended indefinitely in each direction to allow us to represent the entire 3D universe or, at least, enough of the 3D universe as we need for this argument. Using this co-ordinate system, the lab equipment and everything else in the 3D universe can be represented.Location Within Finite Regions of Space
For simplicity sake, we can imagine that there is a wooden box in the laboratory. Inside this box there is space enough for us to place an array of different items. The space inside this box, as enclosed by the boundaries/sides of the box, is a finite 'region of space'.
We can also represent the box mathematically/graphically along with the finite region of space it encloses. We can do this by drawing a cuboid with the corresponding measurements and shading the area inside the cuboid i.e. inside the lines which represent the sides. The shaded area represent the finite region of space, inside the box.
As we mentioned, we can place an array of objects (or systems) inside the box. Something is said to be 'located within the finite region of space [of the box]' if it is anywhere within the shaded area i.e. anywhere inside the box. To illustrate this point, we could place a pregnant cat inside the box and close the lid. Now, we might not be able to represent then exact position of the cat inside the box, but we can say that the cat is, most certainly, 'located within the finite region of space of the box'.
Quantum experiments are somewhat different from putting cats in boxes although thought experiments with cats in boxes can provide useful analogies.
Quantum Experiments
With our experimental set-ups we have a piece of equipment which prepares the quantum system and at some later time, t, we have a measurement outcome on a screen.
One of our assumptions is that the preparation equipment can only exert a causal influence which propagates through 3D space at a maximum speed c i.e. the speed of light and that any system created by the preparation device can travel no faster than c. If this is the case, then that allows us to define a finite region/volume of 3D space* within which the system prepared by the device must be located. If it were possible to measure the system outside this finite region of space i.e. if there were a non-zero probability of measuring it outside this region, that would necessitate that the system had traveled FTL or that it does not operate in 3D space.
*a sphere with radius ct.
Possible Paths
There are an infinite number of possible paths from the preparation device to the measured outcome and we could, theoretically, represent those infinite number of possible paths, graphically. Some of those would all fall within our sphere of radius ct. Those that fall within the sphere represent the possible paths a system limited to the speed of light could take.
Intuitively, we might think of the paths taken being those of a point particle [with a definite position and momentum], but we can't necessarily do that for quantum systems. Instead, what we can say is that whatever path the system took, from preparation device to measured position, it must have been within the finite region of space enclosed by the sphere with radius ct.
To say that something 'passes through' the finite region of space we simply mean:
1) it took one of the possible paths within the finite region of space enclosed by the sphere
2) it took every possible path within the finite region of space enclosed by the sphere
3) it too more than one possible path within the finite region of space enclosed by the sphere.
If the possible paths of the system from preparation device to measured position must fall within the sphere of radius ct, then we can say with certainty, that the system was located within the finite region of space i.e. that its position was somewhere within that finite region of space. Where position doesn't have to take a single, pre-defined value.
In the case of the Stern-Gerlach experiement, we can set-up two SG magnets (A and B) and two detector screens. But we need use only one preparation device. We can define (and graphically represent) the finite regions of space occupied by the different magentic fields. If we can say the system 'passes through' the region of space occupied by magetic field A but doesn't 'pass through' the adjacent magnetic field B, then we can narrow down the position/location of the system to the finite region of space occupied by magnet A.
Probability of Position
There is a difference between the following statements:
1) There is a non-zero probability of measuring the system in position X.
2) The system is in position X with a probability of 1 or 0.
As mentioned, we can [in principle] represent all possible paths the system could have taken from preparation device to measured outcome. These don't have to be the paths of a point particle with definite position and momentum. There are possibly an infinite number of such paths, but the probability that the system took each path is either 1 or 0 i.e. it either took Path 1, or it didn't; it either took path 2 or it didn't. This is true if the system operates in 3 dimensional space.
This means that prior to measurement, for any possible position within the finite region of space, the system is in that position with a probability of 1 or 0. It is not necessary that the system be in a single, pre-defined positon and that single, pre-defined position only, since it is possible for it to be in multiple positons with a probability of 1.
This is a separate proposition to the probability that when we measure the system it will always be in a single, well-defined position. However, if a system is always in a given positon with a probability of 1 or 0, and cannot be only one single position with a probability of 1, it must be in multiple positions simultaneously. If we always measure it in only one well-defined position then there must be some sort of physical, FTL collapse of the system.
Alternatively, the system does not operate in 3 dimensions.Schroedingers Kittens
To use an analogy. Imagine that we have never witnessed kittens being born before. For some reason, the birthing process only ever seems to occur when we we put a kitten preparation device (i.e. a cat) into a closed, finite region of space e.g. a closed box. We have an intuitive idea about how the birthing process works but our calculations tell us that cats giving birth to kittens don't behave the same way that other animals do.
So, we put the pregnant cat in the box and we know that at some time t when we open the box, we will find a single kitten in a well defined position inside the box. But, prior to opening the box we don't know what the position of the kitten is. However, we know for absolute certain that it must have some position inside the box. The probability of the position of the kitten in the box cannot be 0 everywhere in the box, it must be 1 in at least one position.
Our calculations tell us that it cannot be 1 in just one position, so therefore, it must be 1 in multiple positons. Otherwise, the birthing process does not occur in only 3 dimensions.