RLC circuit resonance experiment

[Shreya]

Homework Statement

I tried to perform an experiment in my school physics lab with an RLC circuit. I plotted the variation of voltage across resistor against frequency of source.

Relevant Equations

Frequency of resonance $\omega^2 = \frac {1} {LC}$

From the graph below of voltage across resistor vs. source frequency, it can be seen that resonance is obtained at 828Hz. But, on calculating the inductance of my inductor (homemade) using $\frac {1}{(2\pi f)^2C}$, I got 7.9mH. But this is greater than the inductance of the solenoid calculated using $L=\mu n^2 Al$, where $\mu$ is permeability of vacuum, A is the cross-section of solenoid, l is the length of solenoid and n is the number of turns per unit length . Could someone please help me understand why. Please be kind to help.

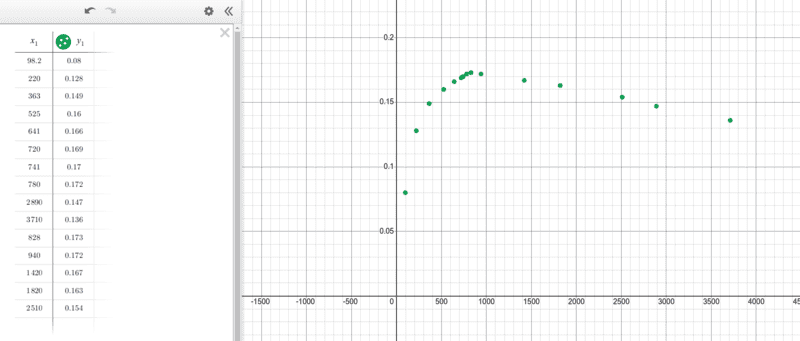
The capacitor i used was rate $4.7 \micro farad$.

 

[BvU]

Hello,

Your post appears somewhat incomplete to me:

• what circuit ?
• What C value ?
• $\mu,\ n, \ A, \ l$ ?
• what is $x,\ y$ ?

You leave us guessing (I could reverse-engineer some things, but that's generally only asking for confusion).

Perhaps it's a good idea to read the PF guidelines ....

Oh, and it's $\omega^2 = \frac {1} {LC}$ ...

$\$

 

[Shreya]

Sorry for that, I have edited my question. Also here is a pic of my homemade inductor.

 

[BvU]

I have edited my question.

Good. Makes my post look foolish, but never mind.

Leaves me wondering:
what is this

?

what is this

?

what is this

?

And

• μ, n, A, l ?
• what is x, y ?

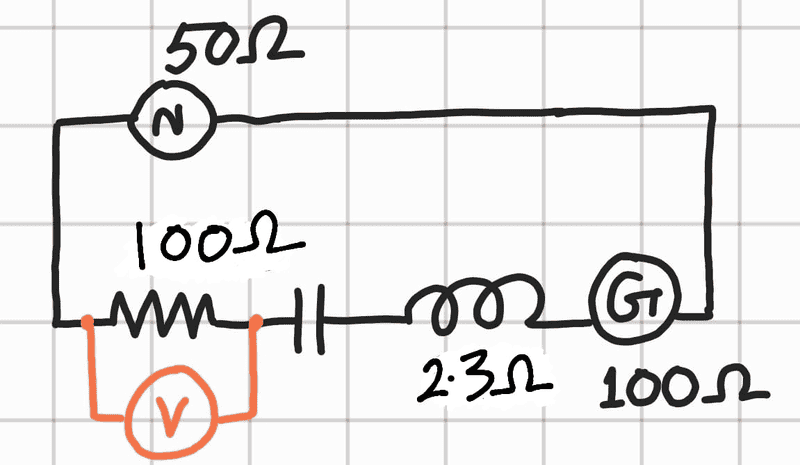
The capacitor I used was rated 4.7$\mu$F.

Good 2. (followed from $f$ and the 7.9 mH)

Your $L=\mu n^2 Al$ agrees with this but you don't mention the values you inserted, nor the result, so there's no way to check.

$\$

 

[Shreya]

Those images are a galvanometer (with 100 ohms resistance), my inductor (with 2.3 ohm resistance) and the ac source (which had 50 ohm resistance). I am sorry, i accidentally wrote the wrong resistances, i will edit the image.

Also here is my calculations. Hope this is better. Thank you for your patience

 

[Shreya]

Wait a minute, now that i think about it, the moving coil galvanometer must have had some inductance, right? That must be the reason of my higher value of calculated inductance

 

[nasu]

The formula for the solenoid works for solenoid, which is supposed to be an ideal model with infinite length and only one layer of wire wrapped around the core. If not infinite, the ratio diameter to length should be much smaller than 1. Your coil does not seem to satisfy any of these conditions. So, why would you expect to follow that formula?

 

[Shreya]

Thanks @nasu. That makes sense.

 

[BvU]

Ok, so calculation result reproduced -- except it's 0.6 mH, not 0.6 mF.
(But where does the 3.84 cm come from ? The picture suggests a lower value !)

Wait a minute, now that i think about it, the moving coil galvanometer must have had some inductance, right? That must be the reason of my higher value of calculated inductance

Good observation ! It makes one wonder what the galvanometer is doing there ! Its inductance is indeed in series with your coil.
So you are missing 7.3 mH that maybe you can find back in the information about the galvanometer ?

This thread is a clear statement that one should always evaluate lab results immediately. Maybe not with all the statistics and details, but at least order-of-magnitude and a preliminary result.

 

[Shreya]

(But where does the 3.84 cm come from ? The picture suggests a lower value !)

I will check on that. Thanks for pointing it out!

This thread is a clear statement that one should always evaluate lab results immediately. Maybe not with all the statistics and details, but at least order-of-magnitude and a preliminary result.

That's true! Will do that from next time.
Thanks a million @BvU. Your suggestions really helped me figure out the issue.

 

[berkeman]

Wait a minute, now that i think about it, the moving coil galvanometer must have had some inductance, right? That must be the reason of my higher value of calculated inductance

If you are just wanting to understand/verify some calculations for the resonance of a real RLC circuit, I'd leave out the galvanometer since it adds nothing useful to the circuit. If you want to know the current, you already have that in your measurement of the voltage across the resistor.