RLC Series Network: Impedance, Current, Power Factor, Phasor Diagram

[Ben_Walker1978]

Homework Statement

RCL Series Network

Relevant Equations

Ohms Law

Hello.

I have completed the following question.

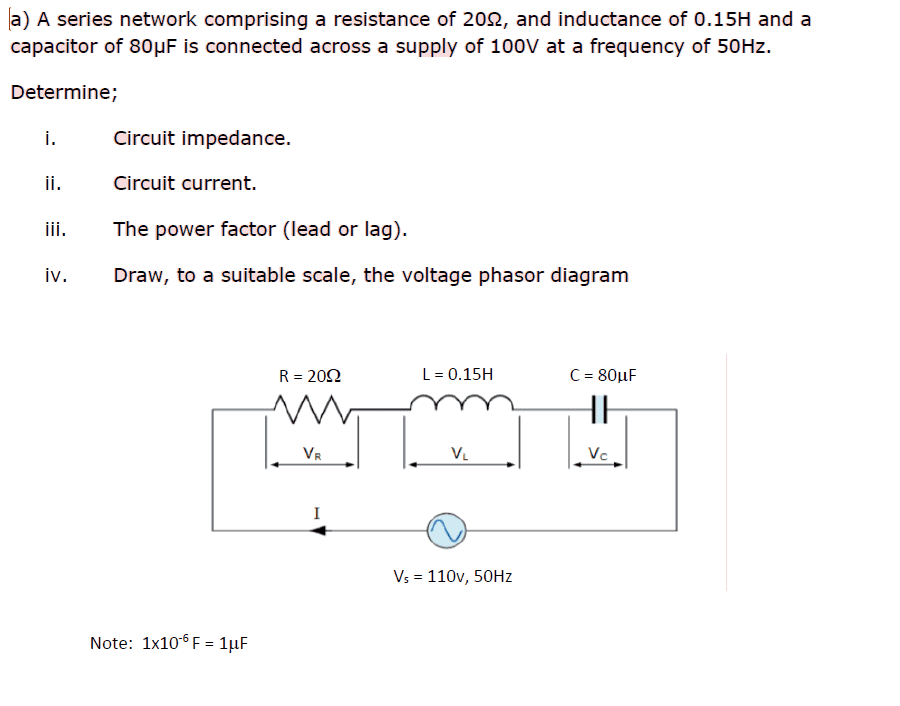
My answer:

i)

Circuit Impedance

Reactance = XL = 2 x pi x F x L
= 2 x pi x 50 x 0.15
= 47.12 Ohms

Reactance of Capacitor = XC = 1/2 x pi x F x C
= 1/2 x pi x 50 x 80x10^-6
= 0.0006366 Ohms
Total reactance = XT = 47.12 - 0.0006366
= 47.119 Ohms
Z^2 = R^2 + XT^2
= 20^2 + 47.199^2
= 2,620.200161
Square Root of 2,620.200161 = 51.187 Ohms

Z = 51.187 Ohms

Theta = Tan^-1 (47.119/20) = 67 Degrees

ii)

Circuit current

Ohms Law

I = V/Z = 100/51.187
= 2.14 Ohms

0 Degree - 67 = -67 Degree

2.14 > -67 Degree

iii)

The Power Factor

PF = True Power / Apparent Power

R = Resistance
Z = Impedance

PF = CosTheta = R/Z
= 20/51.187
= 0.390

I have this so far. Trying to learn and complete this question. Once i know these answers are correct i will draw the phasor diagram.

Any help will be much appreciated.

I think i have done all this correct. Just asking to make sure i haven't made any mistakes.

Thanks

 

[ammarb32]

You made a mistake when you were calculating the reactance of the capacitor. The correct formula to find th reactance of a capacitor is:

Also, when you are calculating the circuit current in (ii), the unit of current is in "Amperes" or just noted as "A" at the end of the current value.Just to confirm, is the voltage source 100V or 110V? In the diagram it says 110V, but in the problem statement, it says 100V.It's important to mention whether the Power Factor is leading or lagging. A "leading" power factor means that the current phase value (i.e. the current "angle") in the circuit is larger than the voltage phase value (i.e. the voltage "angle") in the circuit. That will help you when you are drawing the phasor diagram to know which one is leading/lagging the other.

 

[Ben_Walker1978]

Thank you for your reply.

I had the reactance of capacitor formula correct.

I have calculated this. Is this correct? If not where have i gone wrong?

Reactance of Capacitor = XC = 1/2 x pi x F x C
= 1/2 x pi x 50 x 80x10^-6
= 0.006283 Ohms

I will put A after circuit current

I will find out whether it is 100 or 110V

And the power factor is lagging.

Thank you for helping me.

Much appreciated.

 

[ammarb32]

Thank you for your reply.

I had the reactance of capacitor formula correct.

I have calculated this. Is this correct? If not where have i gone wrong?

Reactance of Capacitor = XC = 1/2 x pi x F x C
= 1/2 x pi x 50 x 80x10^-6
= 0.006283 Ohms

I will put A after circuit current

I will find out whether it is 100 or 110V

And the power factor is lagging.

Thank you for helping me.

Much appreciated.

You are supposed to put the 2 * pi * f * C in the denominator.

It's supposed to be like this:

It seems that you plugged the equation into your calculator incorrectly by doing this:

 

[Ben_Walker1978]

I thought i was doing it wrong!

Thank you so much for that

 

[Ben_Walker1978]

i)

Circuit Impedance

Reactance = XL = 2 x pi x F x L
= 2 x pi x 50 x 0.15
= 47.12 Ohms

Reactance of Capacitor = XC = 1/2 x pi x F x C
= 1/2 x pi x 50 x 80x10^-6
= 39.7887 Ohms
Total reactance = XT = 47.12 - 39.7887
= 2.3313 Ohms
Z^2 = R^2 + XT^2
= 20^2 + 2.3313^2
= 405.43
Square Root of 405.43 = 20.13 Ohms

Z = 20.13 Ohms

Theta = Tan^-1 (20.13/20) = 1 Degrees

ii)

Circuit current

Ohms Law

I = V/Z = 100/20.13
= 4.96 Ohms

0 Degree - 1 = -1 Degree

4.96 > -1 Degree

iii)

The Power Factor
PF = True Power / Apparent Power

R = Resistance
Z = Impedance

PF = CosTheta = R/Z
= 20/20.13
= 0.99

Is this now correct?

I have correct all by calculating the Z correctly

Your help is very much appreciated

 

[ammarb32]

i)

Circuit Impedance

Reactance = XL = 2 x pi x F x L
= 2 x pi x 50 x 0.15
= 47.12 Ohms

Reactance of Capacitor = XC = 1/2 x pi x F x C
= 1/2 x pi x 50 x 80x10^-6
= 39.7887 Ohms
Total reactance = XT = 47.12 - 39.7887
= 2.3313 Ohms
Z^2 = R^2 + XT^2
= 20^2 + 2.3313^2
= 405.43
Square Root of 405.43 = 20.13 Ohms

Z = 20.13 Ohms

Theta = Tan^-1 (20.13/20) = 1 Degrees

ii)

Circuit current

Ohms Law

I = V/Z = 100/20.13
= 4.96 Ohms

0 Degree - 1 = -1 Degree

4.96 > -1 Degree

iii)

The Power Factor
PF = True Power / Apparent Power

R = Resistance
Z = Impedance

PF = CosTheta = R/Z
= 20/20.13
= 0.99

Is this now correct?

I have correct all by calculating the Z correctly

Your help is very much appreciated

When you were calculating your Total Reactance:

Total reactance = XT = 47.12 - 39.7887
= 2.3313 Ohms

It should actually be 7.3313 ohms.

 

[Ben_Walker1978]

i)

Circuit Impedance

Reactance = XL = 2 x pi x F x L
= 2 x pi x 50 x 0.15
= 47.12 Ohms

Reactance of Capacitor = XC = 1/2 x pi x F x C
= 1/2 x pi x 50 x 80x10^-6
= 39.7887 Ohms
Total reactance = XT = 47.12 - 39.7887
= 7.3313 Ohms
Z^2 = R^2 + XT^2
= 20^2 + 7.3313^2
= 453.74
Square Root of 453.74 = 21.3 Ohms

Z = 21.3 Ohms

Theta = Tan^-1 (21.3/20) = 1 Degrees

ii)

Circuit current

Ohms Law

I = V/Z = 100/21.3
= 4.69 Ohms

0 Degree - 1 = -1 Degree

4.69 > -1 Degree

iii)

The Power Factor
PF = True Power / Apparent Power

R = Resistance
Z = Impedance

PF = CosTheta = R/Z
= 20/21.3
= 0.938

That was me putting in the calculator incorrect.

Thank you for notcing that.

The only thing is my degree correct in ii)?

 

[ammarb32]

i)

Circuit Impedance

Reactance = XL = 2 x pi x F x L
= 2 x pi x 50 x 0.15
= 47.12 Ohms

Reactance of Capacitor = XC = 1/2 x pi x F x C
= 1/2 x pi x 50 x 80x10^-6
= 39.7887 Ohms
Total reactance = XT = 47.12 - 39.7887
= 7.3313 Ohms
Z^2 = R^2 + XT^2
= 20^2 + 7.3313^2
= 453.74
Square Root of 453.74 = 21.3 Ohms

Z = 21.3 Ohms

Theta = Tan^-1 (21.3/20) = 1 Degrees

ii)

Circuit current

Ohms Law

I = V/Z = 100/21.3
= 4.69 Ohms

0 Degree - 1 = -1 Degree

4.69 > -1 Degree

iii)

The Power Factor
PF = True Power / Apparent Power

R = Resistance
Z = Impedance

PF = CosTheta = R/Z
= 20/21.3
= 0.938

That was me putting in the calculator incorrect.

Thank you for notcing that.

The only thing is my degree correct in ii)?

When you calculate your theta using tan^-1 (21.3 / 20), you get 1 degree:

When I plug in tan^-1 (21.3 / 20), I get 46.80 degrees (Please see screenshot below):

 

[ammarb32]

When you calculate your theta using tan^-1 (21.3 / 20), you get 1 degree:
View attachment 263225When I plug in tan^-1 (21.3 / 20), I get 46.80 degrees (Please see screenshot below):

View attachment 263224

Actually, sorry I made a mistake.

Please see the file I attached at the bottom of this post (PF calculation.pdf attached). This file shows the full work of the problem that I did. Your reactance calculations (for the inductor and capacitor) are correct. It's just that you made a mistake when you calculated the impedance angle.

When you are calculating your impedance angle, you are meant to use the Imaginary part of the Impedance divided by the Real Part of the Impedance and then do the tan^-1 of that (You can see the calculation in the file I attached containing my work).

However, you are using the "Magnitude" of the impedance in your solution:

Essentially, you calculated the impedance angle this way:

The correct way to calculate the impedance angle is this way:

Also, when you are calculating your Power Factor, it is better to use the equation that has the Voltage and Current Angle:

That way, you will know immediately if the Power Factor is "leading" or "lagging". If the phase of the current (i.e. current angle value) is larger than the phase of the voltage (i.e. voltage angle value), that means you will immediately know it is a "leading" PF. However, if the current angle value is lower than the voltage angle value, then that means you know its a "lagging" PF.
This PF equation you used is also correct:

However, it doesn't tell you whether the PF is leading or lagging like the other equation.Also, please remember to put the correct units. I noticed you used "Ohms" when you were calculating your circuit current. I'm assuming you're in undergrad taking a Power Systems/Intro to Circuits course. Your professor/TA will definitely mark you down for this so be careful.

Once you make these corrections, you will be able to draw your phasor diagram.

 

[Ben_Walker1978]

Thank you for that. I am now a little confused. But think i have it below:

I just need some help with the phasor diagram please. I have most of it complete. Just need help finishin git.

i)

Circuit Impedance

Reactance:

XL = 2 · π · F · L

= 2 · π · 50 · 15

= 47.12 Ohms



Reactance of Capacitor:

XC =

=

= 39.7887 Ohms



Total Reactance:

XT = XL – XC

= 47.12 – 39.7887

= 7.3313 Ohms
Z2 = R2 + XT2

= 202 + 7.33132

=453.74



= 21.3 Ohms

Z = 21.3 Ohms
Z = (R) + I (x)

Z = ((20) + I (7.3313))

IZI =

=

= 21.30
ii)

Circuit Current

Ohms Law

tan-1 ()

= tan-1

θ = 20.13°

0
I =

=

= 4.69 Ohms

Circuit Current = I = (4.69)(-20.13°) A

iii)

The Power Factor

PF =

R = Resistance

Z = Impedance

PF =

=

= 0.938

Lagging due to XL > XC



iv)

Phasor Diagram

 

[ammarb32]

Thank you for that. I am now a little confused. But think i have it below:

I just need some help with the phasor diagram please. I have most of it complete. Just need help finishin git.

i)

Circuit Impedance

Reactance:

XL = 2 · π · F · L

= 2 · π · 50 · 15

= 47.12 Ohms



Reactance of Capacitor:

XC =

=

= 39.7887 Ohms



Total Reactance:

XT = XL – XC

= 47.12 – 39.7887

= 7.3313 Ohms
Z2 = R2 + XT2

= 202 + 7.33132

=453.74
= 21.3 Ohms

Z = 21.3 Ohms
Z = (R) + I (x)

Z = ((20) + I (7.3313))

IZI =

=

= 21.30
ii)

Circuit Current

Ohms Law

tan-1 ()

= tan-1

θ = 20.13°

0
I =

=

= 4.69 Ohms

Circuit Current = I = (4.69)(-20.13°) A

iii)

The Power Factor

PF =

R = Resistance

Z = Impedance

PF =

=

= 0.938

Lagging due to XL > XC



iv)

Phasor Diagram

View attachment 263511View attachment 263512

Is there something I can clear up so you're not confused anymore? If you do have any questions please do ask so I can clear them up.

Otherwise, here are some good Phasor Diagram examples you can learn from:

If you go to this link, there is an example of an RLC Circuit (on Page 9 / 18 on the PDF link).

https://www.philadelphia.edu.jo/academics/fobeidat/uploads/Electric Circuits II Course/5 Phasor diagram.pdf
Here's also an example of an RLC Circuit Example on Youtube:

 

[Ben_Walker1978]

No, i think i am all good now.

I will have a look at the phasor video and attempt it.

Thank you for your help.

Much appreciated

 

[Ben_Walker1978]

My attempt at Phasor Diagram after looking at the links you gave. How does this look?? And if I have, where have I gone wrong. Only think I was unsure about is the current added on to he resistor.

 

[ammarb32]

My attempt at Phasor Diagram after looking at the links you gave. How does this look?? And if I have, where have I gone wrong. Only think I was unsure about is the current added on to he resistor.

View attachment 263580

Just to confirm, in the problem statement that you posted, it says draw the "voltage phasor diagram" (screenshot below):

Is this the original problem statement or is there another question asking you to draw the full phasor diagram for the AC circuit?

 

[Ben_Walker1978]

No this is the original problem statement. I just did not read it correctly.

 

[ammarb32]

No this is the original problem statement. I just did not read it correctly.

Ok then in that case you should only draw the voltage phasor diagram. Heres another example of a series RLC Circuit:


Remember when you only draw the voltage phasor diagram, you need to know if the current is leading or lagging the voltage and by how much it is leading or lagging (i.e. the angle value)

 

[Ben_Walker1978]

Thank you.

I have drawn a Voltage Phasor diagram below.

Is this now correct?

 

[ammarb32]

Just to confirm, I have noticed that some conventional voltage phasor diagrams include real and imaginary impedances. I'm assuming you are taking this class in undergrad. Has your professor gone over voltage phasor diagrams? Does your professor/TA require you to include certain parameters in your voltage phasor diagram.

From what I can see, you just need to clearly indicate the magnitude and phase for the voltage and current (Even if it is 0 degrees, you need to write it). So for example, your voltage will need to clearly be written as (110/_0°) Volts and your current needs to be clearly written as (4.69/_-20.13°) A. Otherwise, I think it's correct. You also show which one is leading/lagging the other with the correct angle drawing (Showing the current 20.13° below the voltage).

So please double check that your professor/TA doesn't require you to include any impedances in your voltage phasor diagram. From my understanding, for a voltage phasor diagram, you don't include the impedances (Like you would for a full phasor diagram). If anyone else may have comments on this, please do include them.

 

[Ben_Walker1978]

Hello,

I think it is just the voltage diagram as i have done. I will show them and see what they say. I am a undergrad yes.

So my answer:

i)

Circuit Impedance

Reactance:

XL = 2 · π · F · L

= 2 · π · 50 · 15

= 47.12 Ohms
Reactance of Capacitor:

XC =

=

= 39.7887 Ohms
Total Reactance:

XT = XL – XC

= 47.12 – 39.7887

= 7.3313 Ohms
Z2 = R2 + XT2

= 202 + 7.33132

=453.74
= 21.3 Ohms

Z = 21.3 Ohms
Z = (R) + I (x)

Z = ((20) + I (7.3313))

IZI =

=

= 21.30
ii)

Circuit Current

Ohms Law

tan-1 ()

= tan-1

θ = 20.13°

0
I =

=

= 4.69 Ohms

Circuit Current = I = (4.69)(-20.13°) A

iii)

The Power Factor

PF =

R = Resistance

Z = Impedance

PF =

=

= 0.938

Lagging due to XL > XC
iv)

Phasor Diagram

Is this now correct?

Thank you soo much for your help!

 

[ammarb32]

Hello,

I think it is just the voltage diagram as i have done. I will show them and see what they say. I am a undergrad yes.

So my answer:

i)

Circuit Impedance

Reactance:

XL = 2 · π · F · L

= 2 · π · 50 · 15

= 47.12 Ohms
Reactance of Capacitor:

XC =

=

= 39.7887 Ohms
Total Reactance:

XT = XL – XC

= 47.12 – 39.7887

= 7.3313 Ohms
Z2 = R2 + XT2

= 202 + 7.33132

=453.74
= 21.3 Ohms

Z = 21.3 Ohms
Z = (R) + I (x)

Z = ((20) + I (7.3313))

IZI =

=

= 21.30
ii)

Circuit Current

Ohms Law

tan-1 ()

= tan-1

θ = 20.13°

0
I =

=

= 4.69 Ohms

Circuit Current = I = (4.69)(-20.13°) A

iii)

The Power Factor

PF =

R = Resistance

Z = Impedance

PF =

=

= 0.938

Lagging due to XL > XC
iv)

Phasor Diagram

View attachment 263775

Is this now correct?

Thank you soo much for your help!

So like I said in my previous post, please also double-check with your colleagues/professor because some professors might teach this in a different way. But as far as I know, for a voltage phasor diagram, this should be fine because you don't need to include impedances.

One thing you can also do just to make sure you understand how you arrived at the final voltage phasor diagram, is to draw the individual voltage phasor diagrams for each component in the circuit. So the voltage for the resistor, inductor, and capacitor, you draw the phasor for each one, and then add them to get to the final 110 V (0 degrees). Same thing with the individual current phasors. You draw each of them and show how you added them up to get to the final circuit current phasor.