Roark's Equations for Discontinuity Stresses Syntax

In summary, R_A refers to the radius of common circumference, which is the intersection of the midsurfaces of two different shells. It is measured vertically from an axis bisecting the shell horizontally and can be a function of the radius of one of the shells. R_A is not to be confused with delta R_A, as seen in the table provided.
  • #1
josep233
1
0
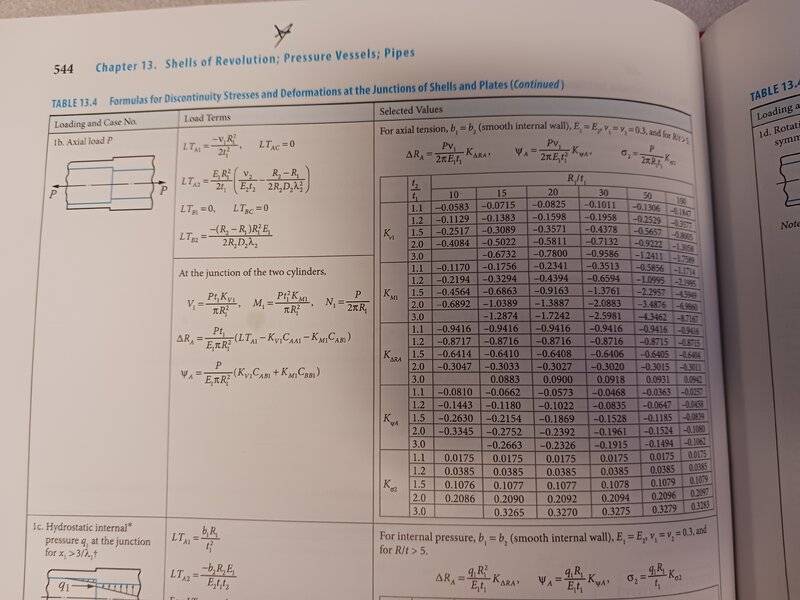
I am looking for clarification of some terms found in Roark's Formulas for Stress and Strain 9E. Table 13.4 pg 543 as well as preceding tables frequently reference R_A as the radius of common circumference. I take this to mean that this value could include any radius that both cylinders share through their thicknesses, but do not know for sure. To further confuse this, some tables say R_A = R_1. Does anyone with more exposure to this understand what R_A means?
20230524_111329.jpg
 
Last edited by a moderator:
Engineering news on Phys.org
  • #2
R_A =radius of common circumference, i.e. it is defined as the intersection of the midsurfaces of the two different shells (not just any shared radius). It is generally defined as a vertical distance from an axis bisecting the shell horizontally. So if the left-most section isn't curved, then R_a should equal R_1.
1686676572241.png


If the left section is e.g. more circular, then the R_a is a function of R_1*sin() -> since R_a is measured vertically in the fashion the diagrams are usually portrayed, not radially.
1686676452828.png

It's maybe worth saying that R_A is not delta R_A, which is all I see in the table you shared.
 
  • Informative
Likes Tom.G

1. What are Roark's Equations for Discontinuity Stresses Syntax?

Roark's Equations for Discontinuity Stresses Syntax are a set of mathematical equations used to analyze the stresses and strains on a material with discontinuities, such as cracks or holes. These equations take into account factors such as the geometry of the discontinuity, the material properties, and the applied loads.

2. Who is Roark and why are these equations named after him?

Roark refers to Richard Southwell Roark, an American engineer who developed these equations in his book "Formulas for Stress and Strain." His work has become a standard reference for engineers and scientists studying the behavior of materials under stress.

3. What types of materials can Roark's Equations be applied to?

Roark's Equations can be applied to a wide range of materials, including metals, plastics, composites, and ceramics. They can also be used to analyze structures made of multiple materials, as long as the material properties are known.

4. How accurate are Roark's Equations for Discontinuity Stresses Syntax?

Roark's Equations are considered to be very accurate, as long as the assumptions and limitations of the equations are taken into account. These include assumptions about the material behavior, the geometry of the discontinuity, and the loading conditions.

5. Are there any limitations to using Roark's Equations for Discontinuity Stresses Syntax?

Yes, there are some limitations to using Roark's Equations. These equations are based on certain assumptions and may not accurately predict the behavior of materials in extreme conditions or situations where the assumptions do not hold. It is important to carefully consider the limitations and validate the results with experiments or other methods.

Similar threads

Roark's formulas for stress and strain
    • Mechanical Engineering
Replies
2
Views
23K
Stress/strain+general bending equation
    • Introductory Physics Homework Help
Replies
4
Views
3K

Hot Threads

Recent Insights

Back
Top