Rocket thrust equation in under-expanded nozzle

[pejsek]

TL;DR Summary

How does the rocket thrust equation work for under-expanded nozzle where the pressure component of thrust becomes positive and thrust should then be higher?

Hello,

so the thrust equation goes like: F = (m dot)*v_e + A_e*(p_e - p_a), where

F ... thrust [N]
m dot ... mass flow rate [kg/s]
v_e ... velocity of exhaust [m/s]
A_e ... area of the exit nozzle plane [m2]
p_e ... pressure of the exhaust at the exit of the nozzle [Pa(a)]
p_a ... ambient pressure [Pa(a)]

We know that if p_e < p_a the pressure component in the equation will be negative and thrust will go down. That is the case of over-expanded nozzle. If p_e = p_a the pressure component is zero and as every rocket physics book says, the flow through the nozzle has reached its optimal condition. This is where thrust and specific impulse reach their maximum.

It is well known that the maximum thrust and specific impulse of a nozzle is in vacuum, as is evident from the picture below taken from the book Fundamentals of Rocket Propulsion by D.P. Mishra.

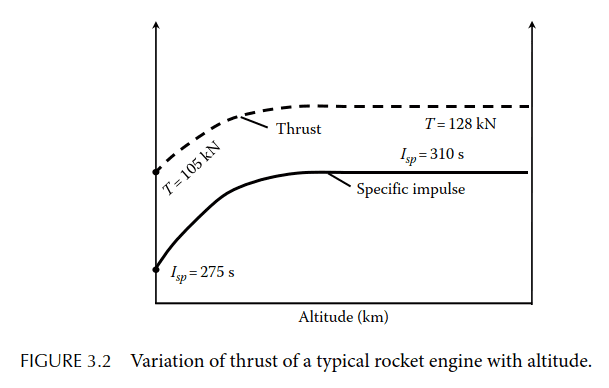
My question is, how does this fact translate into the thrust equation? For p_e > p_a the pressure component would become positive and add some thrust. But clearly that's not what happens. I was thinking maybe v_e gets smaller, but v_e seems to be function of p_e but not p_a, according to this equation:

p_e is affected by p_a though, but only when the nozzle is highly over-expanded and a shock wave occurs inside the nozzle. If p_e > p_a then the exhaust can expand no more inside the nozzle (the nozzle is "too short") and so p_e no longer decreases. In the same book, the author gives this example calculation:

where he adds the pressure component to the total thrust. If we substituted the value p_a = 5.53 kPa with the value p_a = p_e = 105 kPa (I know it's weird) which would be the ideal nozzle condition, then the pressure component of thrust would be zero and apparently the total thrust would be lower. So where is the catch?

Thank you for any replies,
pejsek

 

[Benjies]

The equation you have cited for exhaust velocity is not impacted by atmospheric conditions at all. You make the statement that the exhaust pressure is impacted by atmospheric pressure, and that is incorrect. Regardless of whether you are operating the engine at sea level, or in a vacuum, that exhaust velocity is set in stone.

The corrections and losses to thrust that you are seeking in that equation, actually do not reside in that equation. The answer to your question resides in the even-simpler thrust equation:

You mentioned shock waves occurring in the nozzle impacting all of these models- you are correct. However, the moment shocks are forming in your nozzle and you have flow detachment, you can throw away every single one of the equations you see in this thread. Now you're talking about a state that the engine was not designed for, and it has failed. Time to shrug your shoulders, give up on modeling it, and figure out what went wrong with your engine.

 

[mfb]

You still gain a little bit of thrust as the outside pressure keeps decreasing as your formulas show, but a larger nozzle would increase the exhaust velocity and provide more thrust: The engine becomes inefficient in the sense that it doesn't use the full potential of the propellant.