Role of gain in amplifier's frequency compensation....

[Jony130]

But this subject is intuitive.
Let us examine this case (points A and B are not connected)

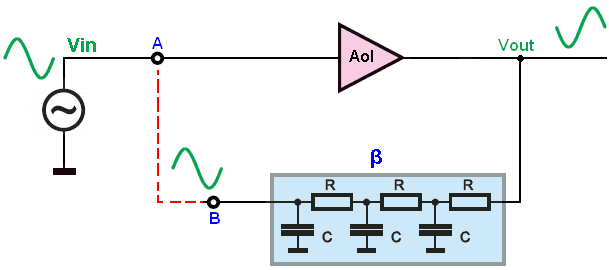
At the beginning we apply input signal (1V) to the input of our inverting amplifier with gain equal to Aol = -29V/V.
The output voltage is of-course equal to Vout = Vin * -Aol = -29V, and we have 180° phase shift between Vin and Vout.

And now, if we add a feedback network which reduces the output signal the the level of the input signal (β = 1/29) and introduces another 180° voltage shift. We will have voltage at point B equal in amplitude and in phase to the input voltage. So now if we disconnect Vin and connect point A with point B we can hope that the circuit will start the oscillations at the frequency where these two conditions (amplitude and phase) are satisfied (Aol*β = 1 at Fo = √6/(2* pi *R*C)).
But if Aol*β < 1 but we meet the phase condition. The circuit will not oscillate because we don't have enough gain in our loop (voltage at point B is smaller than Vin).
And for Aol*β > 1 and phase are identical ( 0° phase shift between Vin and voltage at point B), the circuit will also start the osculation because now we have more gain then we need (Voltage at point B is larger than Vin.). Do you get it ?

 

[LvW]

And for Aol*β > 1 and phase are identical ( 0° phase shift between Vin and voltage at point B), the circuit will also start the osculation because now we have more gain then we need (Voltage at point B is larger than Vin.). Do you get it ?

Yes - I support this view.
Just a short comment: ...will start the oscillation - however, with continuous rising amplitudes until clipping occurs (hard limiting), unless there is another soft-limiting device within the loop (diodes or amplitude-controlled resistors,...).

 

[brainbaby]

we don't have enough gain in our loop (voltage at point B is smaller than Vin).

You have given me a new intuitive insight of the loop gain...I appreciate it...
Loop gain can be thought as Vf/Vin...and that solves all the problem...
So all deal is the loop gain ...if Vin is applied only for one iteration and then the system is realized we found that when loop gain<1 , Vout is attenuated by β and since now Vf is less than Vin, it can be thought of as for the next iteration Vin lowers and hence again this lowered Vin is further attenuated by β network and on and one the cycle perpetuates and the system got stabilised...vice versa when loop gain >1...

Last two questions...

From the beginning you have considered Vin for only one iteration...What would be your explanation when initial Vin is applied for multiple iterations...?
and
This question is somewhat not exactly of scientific temperament...but as we know that multiplication is also a form of addition...i.e its a repetitive addition ...for e.g
4*3=12...
if 4 is added 3 times it leads to 12 ...or if 3 is added 4 times it also leads to 12...
so what difference would if make if loop gain instead of being product of A and B would be the addition of A and B...??
I know it sounds so weird...but its the byproduct of my curiosity...

 

[Jony130]

From the beginning you have considered Vin for only one iteration...What would be your explanation when initial Vin is applied for multiple iterations...?
and

Because this case (only one iteration) is much more easier to understand and to analysis for our brain.

so what difference would if make if loop gain instead of being product of A and B would be the addition of A and B

10 * 1/12 = 0.83
10+1/12 = 10.083

 

[brainbaby]

Jony and LvW...

 

[jim hardy]

Once you have got that intuitive 'feel' for it

it lends new meaning to the old adage

closed loop transfer function = G/(1+GH)

even for the simplest closed loop, taking the case of Mother Nature's favorite shape sinewaves

out = in X 1/(1+1)
out/in = 0.5

Now add delay equal to 180 degrees phase shift at some frequency
180 degrees is just reversing the sign of a sinewave
so what was negative feedback became positive, that is GH became -1
so denominator of G/(1+GH) changes from sum to difference
transfer function becoming G/(1-GH)
out = in X 1/(1-1)
out/in = 1/0
AHA we can have output with zero input !

You saw that in grade school when the PA microphone got just the right distance from speaker to make that awful 'whistle'
that's the distance at which speed of sound over distance from speaker to mic gives delay equal to 180 degrees at the whistle frequency . The immediate fix is to turn down volume reducing loop gain GH below 1.
(New DSP PA systems detect oscillation and change their own settings. I looked for Behringer's specsheet but only found sales stuff from 3rd parties)

Any system in nature , including systems made by man, will find that frequency if one exists. It'll try to enter a state of sine wave oscillation but might shake itself apart first..
hope i wasnt overly redundant..
That little thought experiment locked in the concept for me. I need all the memory aids i can get

old jim

 

[brainbaby]

hope i wasnt overly redundant..

absolutely not Jim...

 

[brainbaby]

Vout still depends on A*k>1 - however, Vout is continuously rising (and the slope of this rising is prop. to A*k) until the voltage is clipped due to a finite supply voltage; hence, we cannot speak anymore of "gain" because the amplifier has left its linear region.

Can you provide me that curve where the slope of rising Vout is prop to loop gain..?? I couldn't google it..

 

[Jony130]

Can you provide me that curve where the slope of rising Vout is prop to loop gain..?? I couldn't google it..

Here you have

 

[LvW]

No - I don`t know if such a curve even does exist. However - why not trying by yourself?
Simulate a simple oscillator circuit (example: WIEN type) for different loop gains (1.1, 1.2,...) and observe the slope of the rising oscillation sgnal.

(Jony130 was quicker by some seconds, congratulations).)

 

[brainbaby]

(Jony130 was quicker by some seconds, congratulations).)

Jony might be celebrating the victory...

 

[LvW]

Can you provide me that curve where the slope of rising Vout is prop to loop gain..?? I couldn't google it..

Hi brainbaby - perhaps the following is interesting for you:
The loop gain is a function in the frequency domain and the slope of the rising oscillation amplitde can be observed in the time domain.
Hence, we need a "connection" of both domains.
This connection does exist in form of the closed-loop poles.
During the starting phase with rising amplitudes the poles of the closed-loop circuit are located in the right half of the s-plane (pos. real part σ).
Because these poles are the solutions of the characteristic equation they also appear as part of the solutions in the time domain.

That means: The oscillation is described by the expression:
Vout(t)=A*exp(s*t)=A*exp(σ+jω)t=A*exp(σt) * exp(jωt)
The first part describes the amplitude (rising for σ>0) and the second part is the sinewave.

As you can see, the pole location (better: The real part of the pole) determines the exponential function which describes the rising amplitudes.
It is the purpose of a nonlinear element in an oscillator to lower the loop gain for large amplitudes and to shift the poles back to the left half of the s-plane (σ<0) withthe consequence of decreasing amplitudes. As a result - the poles will swing between the left and right hallfs of the s-plane - and the amplitude will not be constant but periodically get a bit larger and smaller.

 

[brainbaby]

Hi brainbaby - perhaps the following is interesting for you:
The loop gain is a function in the frequency domain and the slope of the rising oscillation amplitde can be observed in the time domain.
Hence, we need a "connection" of both domains...
...This connection does exist in form of the closed-loop poles.

I'll certainly try to digest your text...but anyway for now your input is required in my following thread...

https://www.physicsforums.com/threa...n-dominant-pole-compensation-strategy.857590/

thanks...!