B Rolling Motion Test: Take the Challenge and Justify Your Answers

[kuruman]

I am posting this to generate a parallel discussion to this ongoing thread. It seems that some participants in that thread have doubts and confusion about rolling motion that might be better addressed separately from the homework problem in question. It is a simple test of one's understanding of forces and torques and rolling motion and is meant for those who are seeking it. My hope is that their participation here by taking the test will help root out their misconceptions, preconceptions and misunderstandings. Of course, all are welcome to contribute.

Test takers: If you choose to answer (any of) the questions, please justify your choice(s). Justifications help diagnose trouble spots.

Statement of the problem
Two strings pull on a wheel of radius $R$ resting on a horizontal surface. The strings apply constant forces $F$ at $R$ and at $R/2$ in opposite directions as shown.

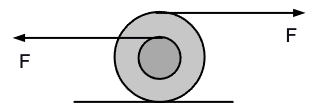
Case 1 The surface is frictionless.
1. In what direction is the acceleration of the center of the disk?
(A) To the left (B) To the right (C) No direction, the acceleration is zero.

2. In what direction does the disk spin/rotate?
(A) Clockwise (B) Counterclockwise. (C) The disk doesn't spin/rotate.

Case 2 There is friction at the surface but no slipping.
1. In what direction is the acceleration of the center of the disk?
(A) To the left (B) To the right (C) No direction, the acceleration is zero.

2. In what direction does the disk spin/rotate?
(A) Clockwise (B) Counterclockwise. (C) The disk doesn't spin/rotate.

3. In what direction is the force of static friction?
(A) To the left (B) To the right (C) No direction, the force of static friction is zero.

 

[DaveC426913]

Case 1:
Q1 = A (Left)
Q2 = A (Clockwise)

The opposing forces generated by the two strings pulling in opposite directions (top one to right, bottom one to left) will act to maximize the horizontal distance between their two attachment points.
Since they're the same magnitude, the net effect is no movement on the centre of the two attachment points, but the wheel itself will be moved to the left:

* see sigline

 

[erobz]

Spoiler: Case 1

Case 1: Question 1: Reply: C

Summing the forces in the horizontal direction:

$$ \sum F = F - F = ma \implies a = 0 $$

Case 1: Question 2: Reply: A

$$ \circlearrowright^+ \sum \tau = R F - \frac{R}{2}F = I \alpha \implies \alpha = \frac{R}{2}F $$

$\alpha$ is positive with respect to the assume convention. Clockwise

 

[malawi_glenn]

the wheel itself will be moved to the left:

Not if the strings are rolled up around the wheel @kuruman perhaps more information is needed regarding the "point of action" and the string.

 

[DaveC426913]

Case 1: Question 1: Reply: C

Summing the forces in the horizontal direction:

I do not think it is sufficient to sum the forces. The wheel is rotating about an axis that is not aligned with its centre, and it is the centre of the wheel that is being asked about.

 

[Orodruin]

I do not think it is sufficient to sum the forces. The wheel is rotating about an axis that is not aligned with its centre, and it is the centre of the wheel that is being asked about.

You just broke Newton’s second law …

 

[DaveC426913]

Not if the strings are rolled up around the wheel @kuruman perhaps more information is needed regarding the "point of action" and the string.

That had not occurred to me. I had assumed the strings were affixed to the wheel at the indicated points..

 

[malawi_glenn]

That had not occurred to me. I had assumed the strings were affixed to the wheel at the indicated points..

anyway, the center of mass will not move if the string was attached around axes at the indicated points either

 

[DaveC426913]

You just broke Newton’s second law …

OK, yeah. I was thinking of the strings as being affixed off-screen.

I think I should have the mods delete my responses as they are detracting from the gist of the thread.

 

[Orodruin]

OK, yeah. I was thinking of the strings as being affixed off-screen.

I think I should have the mods delete my responses as they are detracting from the gist of the thread.

I think it is very much in the geist of the thread:

by taking the test will help root out their misconceptions, preconceptions and misunderstandings.

 

[kuruman]

Not if the strings are rolled up around the wheel @kuruman perhaps more information is needed regarding the "point of action" and the string.

Yes, the strings are wrapped around, one around the circumference of the disk and the other around a shaftof half the radius.

 

[malawi_glenn]

I will steal this for my course, great stuff

 

[jbriggs444]

Case 1:
1: C (acceleration zero, Newton's second)
2: A (Clockwise, it is a clockwise couple)
Case 2:
1: B (acceleration rightward. It is, at least momentarily, a simple lever pushing left on the ground. Newton's third says that the reaction force on the lever is rightward).
2: A (Clockwise, has to be in order for the no-slip condition to be upheld with the rightward acceleration)
3. Both directions. You didn't specify force on the wheel or force on the ground. But the force on the wheel is rightward (B) as already justified above.

Edit: I lose points because I made good choices but wrote down the wrong letters initially. [I'd expected choice B to be clockwise rotation to go along with choice B being rightward motion]

 

[kuruman]

I will steal this for my course, great stuff

Be my guest. You might find the series of rolling motion demos described in this insight worth stealing too. They're fun to do and fun to watch the students' reactions to them.

 

[erobz]

Spoiler: Case 2

I would apply the same system to solve Case 2:

$$ \circlearrowright^+ \sum \tau = F R - \frac{R}{2}F - R \mu m g = I \alpha $$

$$ \mu = \frac{1}{g} a \leq \mu_s $$

$$ \alpha = \frac{a}{R} $$

$$ \implies a = \frac{1}{2} \left( \frac{R^2}{I + mr^2} \right) F $$

$$ \rightarrow ^+ \sum F = F - F + f_r = ma \implies f_r = ma $$

Since $a$ is positive $f_r$ is consistent with the assumed convention.

Case 2 :
Question 1: Reply B - to the right
Question 2: Reply A - Clockwise
Question 3: Reply B - to the right

I'm ready for my lashing!

 

[kuruman]

3. Both directions. You didn't specify force on the wheel or force on the ground. But the force on the wheel is rightward (B) as already justified above.

Sorry, I meant the wheel.

 

[kuruman]

I'm ready for my lashing!

No lashing. Just a remark that you missed some parentheses in the torque equation.

 

[malawi_glenn]

@erobz you do not need go into coefficients of frictions since we are already given that there will be no slipping.

 

[erobz]

@erobz you do not need go into coefficients of frictions since we are already given that there will be no slipping.

Yeah, I see that. I was thinking of it to put a limit on the applied force $F$, but I didn't event follow through with that.

 

[malawi_glenn]

Yeah, I see that. I was thinking of it to put a limit on the force, but I didn't event follow through with that.

Note that f_r = ma is independent of F

 

[erobz]

Note that f_r = ma is independent of F

but $a$ isn't?

$$ a = \frac{1}{2} \left( \frac{R^2}{I + mr^2} \right) F \leq \mu_s g \implies F \leq 2 \mu_s g \left( \frac{I + mR^2}{R^2} \right)$$

 

[Orodruin]

I will steal this for my course, great stuff

This is the type of question that would do well as conceptual questions in a flipped classroom situation. No calculations required and designed to test conceptual understanding.

A common misunderstanding here would likely be that neither rope can extend or be winded up since they are both pulled with the same force. Of course, due to the rotation induced, the inner rope will be wound up and the outer extend.

 

[erobz]

Has anyone ever proposed an actual "test" feature here? You can do this informal testing, but the answers could be revealed quickly. It's hard to take the test when the answer is there already. Or maybe just a "hidden post" that collapses unless clicked on?

Either way, Thanks to @kuruman for setting this up!

 

[jbriggs444]

Has anyone ever proposed an actual "test" feature here? You can do this informal testing, but the answers could be revealed quickly. It's hard to take the test when the answer is there already. Or maybe just a "hidden post" that collapses unless clicked on?

The spoiler tag accomplishes the "hidden post" type stuff.
[SPOILER]like so[/SPOILER]

Spoiler

like so

 

[malawi_glenn]

This is the type of question that would do well as conceptual questions in a flipped classroom situation. No calculations required and designed to test conceptual understanding.

I usually do this kind of discussion question for them, where the rope can be angled in various ways, how and will the spool roll and what happens to the chord if it will unwind or not

 

[erobz]

The spoiler tag accomplishes the "hidden post" type stuff.
[SPOILER]like so[/SPOILER]

Spoiler

like so

Yeah...next time I'll use that in the reply!

 

[kuruman]

I usually do this kind of discussion question for them, where the rope can be angled in various ways, how and will the spool roll and what happens to the chord if it will unwind or not

You might wish to try the trike trick. Loop a string around each pedal, and ask for predictions which way the trike will move when you pull (a) on the "pedal up" string (yellow arrow) and (b) on the "pedal down" string (red arrow).

Note: The handle bars will have to be constrained from turning about the vertical pivot.

Spoiler

(a) In the direction of the yellow arrow.
(b) In the direction of the red arrow.

The teaching comes when you ask, "then how come that when I sit on the trike and push on the 'down' pedal, the bike goes in reverse?"

 

[malawi_glenn]

You might wish to try the trike trick.

I will, when my son is old enough to have such bike :D he is just 3 months now, or I take the opportunity to buy such for the physics lab at my school...

I have taught rotational mechanics at uni, like 10 years ago. Nowadays I teach it to final year high-school students who have a special interest in physics. Thus I need to keep things on a more conceptual level and not do full blown vector calculus stuff. Have not been doing it for that many years so all of these conceptual questions and demonstrations are worth gold

 

[Chenkel]

So after doing some research I found that for any rigid body, the sum of all external forces to the body is equal to the mass of the body times the acceleration of it's cm. I believe this is true (correct me if I'm wrong) even if the external forces create a torque on the body. This is difficult for me to understand because it means if we apply an impulse directly to the center of mass of the body it will have create a certain acceleration for the cm, now if we apply the same impulse off center such that we create a torque, it will have the same acceleration for the center of mass, but now it will also have an angular acceleration too, does anyone know why there seems to be more energy in the body with the same impulse in the off center force example? It seems that something isn't quite adding up. Let me know what you guys think, thank you!

 

[Chenkel]

So after doing some research I found that for any rigid body, the sum of all external forces to the body is equal to the mass of the body times the acceleration of it's cm. I believe this is true (correct me if I'm wrong) even if the external forces create a torque on the body. This is difficult for me to understand because it means if we apply an impulse directly to the center of mass of the body it will have create a certain acceleration for the cm, now if we apply the same impulse off center such that we create a torque, it will have the same acceleration for the center of mass, but now it will also have an angular acceleration too, does anyone know why there seems to be more energy in the body with the same impulse in the off center force example? It seems that something isn't quite adding up. Let me know what you guys think, thank you!

Perhaps I should start a new thread for this problem.