- #1
assaftolko
- 171
- 0
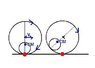
We are given with an hollow thin cylinder that has a mass of M and radius R, and a full cylinder that has a mass of m and radius r. The full cylinder is glued to the bottom of the hollow cylinder
(As in the picture - ignore the speed v0 that is drawn in the picture) and now the hollow cylinder can roll without slipping on the floor while the full cylinder is glued to it from the inside. In order for this system to move - they push slightly to the right the full cylinder so that its center has a speed of v in that direction.
What is the horizontal speed of this system's center of mass just as it starts to move?
I really don't have any idea how to solve this problem... I read something about using the Instant centre of rotation in order to solve this problem but I don't know what it is... until now I alwyas could solve pure roll questions using the fact that the axis of rotation went through the center of mass of the pure rolling body. I'd like to know how can I solve this problem using only the actual axis of rotation, starting with where does it go through... And if there's no choice but to solve this problem using the Instant centre of rotation concept, I'd like to know how does it come to hand for this question...
Thanks a lot!
(As in the picture - ignore the speed v0 that is drawn in the picture) and now the hollow cylinder can roll without slipping on the floor while the full cylinder is glued to it from the inside. In order for this system to move - they push slightly to the right the full cylinder so that its center has a speed of v in that direction.
What is the horizontal speed of this system's center of mass just as it starts to move?
I really don't have any idea how to solve this problem... I read something about using the Instant centre of rotation in order to solve this problem but I don't know what it is... until now I alwyas could solve pure roll questions using the fact that the axis of rotation went through the center of mass of the pure rolling body. I'd like to know how can I solve this problem using only the actual axis of rotation, starting with where does it go through... And if there's no choice but to solve this problem using the Instant centre of rotation concept, I'd like to know how does it come to hand for this question...
Thanks a lot!