- #1
sAXIn
- 12
- 0
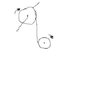
Problem Sketch
Okay so this is the problem the upper disk will be of M1 mass and R1 radius
both disk are solid so I(oe)=1/2MR^2 , the second disk will be HM2 , HR2.
After system is left from rest I understand that the lower disc will start rotating and going down from the rope also it has linear acceleration down because the string is going down from upper disc.
I wrote sigma tau for both discs and sigma Y for the lower one but I need to express TA, Alfa 1 , Alfa 2 and A2 (linear acceleration of second disc)
(alfa -=> angular acceleration )! all of them should be written without being expressed by others.
I can't also figure out why when I express alfa2 by sigma moments on point where the string is leaving the disc it isn't equal to alfa2 by sigma moments on center of disc.
Thank's in advance for help .
Okay so this is the problem the upper disk will be of M1 mass and R1 radius
both disk are solid so I(oe)=1/2MR^2 , the second disk will be HM2 , HR2.
After system is left from rest I understand that the lower disc will start rotating and going down from the rope also it has linear acceleration down because the string is going down from upper disc.
I wrote sigma tau for both discs and sigma Y for the lower one but I need to express TA, Alfa 1 , Alfa 2 and A2 (linear acceleration of second disc)
(alfa -=> angular acceleration )! all of them should be written without being expressed by others.
I can't also figure out why when I express alfa2 by sigma moments on point where the string is leaving the disc it isn't equal to alfa2 by sigma moments on center of disc.
Thank's in advance for help .