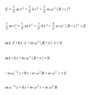kekpillangok
- 15
- 2
- Homework Statement
- Consider a simple harmonic oscillator made of a spring of elastic constant k fixed at one end and having a particle of mass m attached to the other. The oscillator rotates in a horizontal plane with constant angular speed ω round the fixed end, while keeping its motion along the radial direction, as shown in the image. If R_0 is the equilibrium position of the oscillator when ω = 0, show that the square of the angular frequency of the oscillator, for the situation shown in the image, varies linearly with the square of the angular speed ω.
- Relevant Equations
- F_s = kx (spring force)
F_cp = m*(ω^2)*r (centripetal force)
If I understand the problem correctly, I need to find the angular frequency of the mass's oscillations about the radius R, which, I think, should be the length of the spring when the mass is merely rotating with angular speed ω (and not oscillating along the radial direction). I was able to find this new equilibrium position—it is ## R =\frac{R _{0 }}{1 -\frac{m {\omega }^{2 }}{k }} ##. But this doesn't seem to be of much use in finding the angular frequency of the oscillations.
It seems that I have to look at the motion of the mass from the point of view of a rotating frame of reference. I'm quite lost as to how this should be done. If there were no rotation, I would get $$ k x =m {\omega _{0 }}^{2 }x $$, where ##{\omega _{0 }}^{2 }=\sqrt{\frac{k }{m }} ##. Now, however, we have an additional force that is equal to ##F _{centrifugal }=m {\omega }^{2 }{\left( R +x \right) } ##. So the resultant force should be $$ F _{net }=m {\omega }^{2 }{\left( R +x \right) }+k x =m {\omega '}^{2 }x $$ (where I set the whole equal to ##m {\omega '}^{2 }x ##, assuming the resulting motion is simple harmonic motion)?
I don't feel confident writing the non-inertial form of Newton's Second Law for this problem. If anyone can guide me on how I should think about this situation, I will be very grateful.

It seems that I have to look at the motion of the mass from the point of view of a rotating frame of reference. I'm quite lost as to how this should be done. If there were no rotation, I would get $$ k x =m {\omega _{0 }}^{2 }x $$, where ##{\omega _{0 }}^{2 }=\sqrt{\frac{k }{m }} ##. Now, however, we have an additional force that is equal to ##F _{centrifugal }=m {\omega }^{2 }{\left( R +x \right) } ##. So the resultant force should be $$ F _{net }=m {\omega }^{2 }{\left( R +x \right) }+k x =m {\omega '}^{2 }x $$ (where I set the whole equal to ##m {\omega '}^{2 }x ##, assuming the resulting motion is simple harmonic motion)?
I don't feel confident writing the non-inertial form of Newton's Second Law for this problem. If anyone can guide me on how I should think about this situation, I will be very grateful.