Rotating Vector Spherical Harmonics Solutions

[Gwinterz]

Hello,

I am looking for some direction to books or papers which may help me,

When you solve the Helmholtz equation you end up with vector spherical harmonics as solutions. The Helmholtz equation is invarient under rotations which means that rotations of these solutions are also solutions.

I am looking for a way to rotate these solutions, for example around the y-axis by some angle β.

The solutions look like:

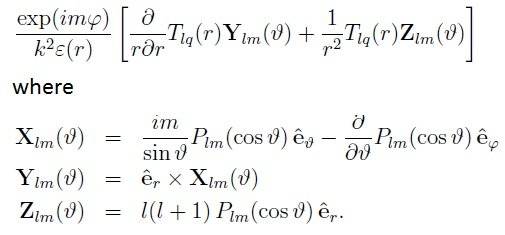
So far all that I have been able to find is that rotations of these solutions can be expressed as a linear combination of them over different l's. What I am unsure about is what the weighting is of this linear combination. I have found some people state that it is the Wigner D function (with an unhelpful reference), but after doing the calculations it doesn't seem like these work as I would have expected.

It's hard for me to distinguish between bad coding and bad intuition at the moment because I haven't found much information about such rotations online.

Is the Wigner D function the correct waiting? Are there some other rotation matrix elements that I should be using as the weighting? Does anyone know of anywhere I could find some more information to learn this properly?

Any help is greatly appreciated,

Thanks

 

[chiro]

Hey Gwinterz.

Rotation matrices have the property that the determinant is 1 and that R^t = R^(-1) (transpose and inverse).

You can construct a general rotation around an axis using a standard matrix and you can also use quaternions if you want to interpolate between rotations on the unit sphere.

Basically these matrices can be expanded for each component and this will give you the general components for the final vector in terms of parameters like an axis and angle or something else.

Aside from this, you could use the tensor formulation and simply use two different co-ordinate systems that are related by the change of basis matrix - the metric tensor.

I don't know what experience you have so I'll just leave it at that.

 

[Gwinterz]

Hey Chiro,

Thanks for your reply,

I think the matrix you may be referring too, or at least in my application, is the Wigner D matrix, in which the Wigner D function takes its form.

Basically what the problem I have been having is, is that I've been questioning if this is the correct rotation matrix.

I collaborated with some people who have done similar calculations recently and they have informed me that they too used this Wigner D function.

For example, referring to the harmonic X, in the picture of my first post, if you were to write this in another set of co-ordinates it would look like this:

Or in Mathematica talk,

The problem I have now is that if I plot the norm of the original harmonic as well as the norm of the rotated harmonic, not only is the function not rotated by the amount I tell it too, but there is a larger (factor of 100) drop in the maximum value of the norm.

Instead of the peak shifting by 1, it only shifts by a little, and as you can see there is a large drop in the magnitude of the norm.

Can you see something that I'm doing incorrectly? I don't think the size of the norm should drop at all, it should be the same no matter what rotation is made.

 

[chiro]

One suggestion I have is to use matrix multiplication instead of using the summation.

What are the structures of your variables? Rotating a vector should return a vector so I'm assuming your calculating linear combinations of your vector with respect to your rotation matrix.

It's a lot easier to check the matrix because you can also check the determinant as well as the orthogonality condition (if it must hold).

You can use your WignerD function to populate the matrix and then you can print the matrix and its contents to see if it comes out right. You can also check the other properties (like determinant of +1 and R^t = R_inv) to make sure it is a rotation matrix.

 

[Gwinterz]

That's a great idea, thanks for that, will try it out!

 

[Gwinterz]

For anyone who ever has this problem,

Generate your VSH's in Mathematica using the SphericalHarmonicY function, rather then LegendreP[..., Cos[theta]]. Even though the functions are essentially the same for thi = 0, up to normalisation, for some reason the rotation does not work...