- #1
WhiteHaired
- 17
- 0
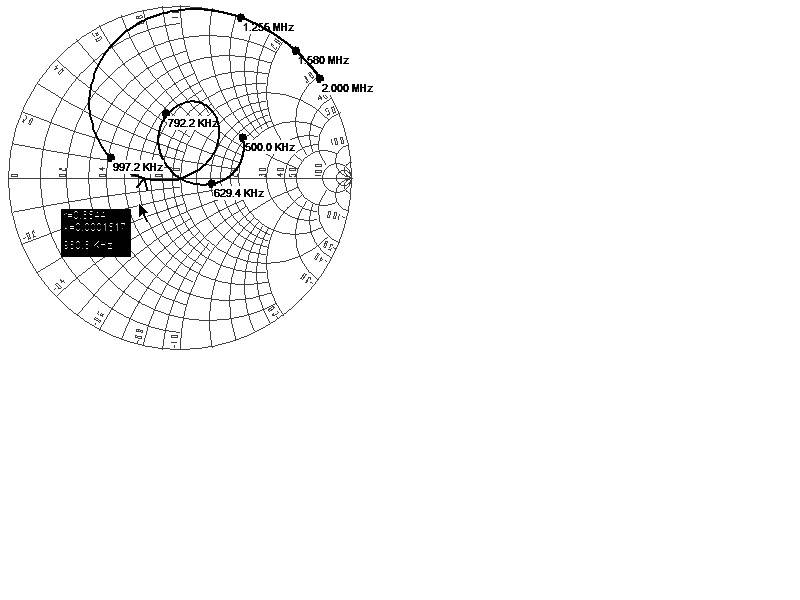
It is always considered that the evolution of the input reflection coefficient, [itex]ρ[/itex], of a LTI causal passive system with frequency, [itex]f[/itex], always presents a local clockwise rotation when plotted in cartesian axes [itex](Re(ρ), Im(ρ))[/itex], e.g. in a Smith chart, as shown in the attached figure.
It must appointed that the local clockwise rotation should not be confused with the derivative of the phase with frequency, which is always negative when the curve encompasses the center of the Smith chart, but it may be positive otherwise (e.g. in a resonant series RLC circuit with R>Z0, where Z0 is the port characteristic impedance). The question here concerns the local rotation, which is always clockwise.
For lossless systems, it may be explained from the Foster’s reactance theorem, “The imaginary immittance of a passive, lossless one-port monotonically increases with frequency”, which has been demonstrated in different ways in literature. It also applies for the reflection coefficient, since the bilinear transform (from immitance to reflection coefficient) preserves orientation.
However I couldn’t find any rigorous proof for lossy systems. Books and manuscripts always reference the lossless case and the Foster’s theorem.
Do you know any reference?
In geometry, for a plane curve given parametrically in Cartesian coordinates as [itex](x(f),y(f))[/itex], the signed curvature, [itex]k[/itex], is
[itex]k=\frac{x'y''-y'x''}{(x^{2}+y^{2})^{3/2}}[/itex]
where primes refer to derivatives with respect to frequency [itex]f[/itex]. A negative value means that the curve is clockwise. Therefore, the reflection coefficient of a LTI causal passive system with frequency, [itex]f[/itex], has always a negative curvature when plotted in Cartesian coordinates [itex](Re(ρ), Im(ρ))[/itex], i.e., it satisfies:
[itex]\frac{∂Re(ρ)}{∂f}\frac{∂^{2}Im(ρ)}{∂f^{2}}<\frac{∂Im(ρ)}{∂f}\frac{∂^{2}Re(ρ)}{∂f^{2}}[/itex]
or, equivalently,
[itex]\frac{∂}{∂f}\left[\frac{\frac{∂Im(ρ)}{∂f}}{\frac{∂Re(ρ)}{∂f}}\right]<0[/itex]→[itex]\frac{∂}{∂f}\left(\frac{∂Im(ρ)}{∂Re(ρ)}\right)<0[/itex]
The same would apply to the complex impedance Z=R+j*X, (or admittance), i.e., [itex]\frac{∂R}{∂f}\frac{∂^{2}X}{∂f^{2}}<\frac{∂X}{∂f}\frac{∂^{2}R}{∂f^{2}}[/itex] and [itex]\frac{∂}{∂f}\left(\frac{∂X}{∂R}\right)<0[/itex]
Is all this right?
Do you know any theorem, property of LTI causal passive systems, energy considerations from which one may conclude this? Kramer-Kronig relations or Hilbert transform?
I would appreciate your help on this.
It must appointed that the local clockwise rotation should not be confused with the derivative of the phase with frequency, which is always negative when the curve encompasses the center of the Smith chart, but it may be positive otherwise (e.g. in a resonant series RLC circuit with R>Z0, where Z0 is the port characteristic impedance). The question here concerns the local rotation, which is always clockwise.
For lossless systems, it may be explained from the Foster’s reactance theorem, “The imaginary immittance of a passive, lossless one-port monotonically increases with frequency”, which has been demonstrated in different ways in literature. It also applies for the reflection coefficient, since the bilinear transform (from immitance to reflection coefficient) preserves orientation.
However I couldn’t find any rigorous proof for lossy systems. Books and manuscripts always reference the lossless case and the Foster’s theorem.
Do you know any reference?
In geometry, for a plane curve given parametrically in Cartesian coordinates as [itex](x(f),y(f))[/itex], the signed curvature, [itex]k[/itex], is
[itex]k=\frac{x'y''-y'x''}{(x^{2}+y^{2})^{3/2}}[/itex]
where primes refer to derivatives with respect to frequency [itex]f[/itex]. A negative value means that the curve is clockwise. Therefore, the reflection coefficient of a LTI causal passive system with frequency, [itex]f[/itex], has always a negative curvature when plotted in Cartesian coordinates [itex](Re(ρ), Im(ρ))[/itex], i.e., it satisfies:
[itex]\frac{∂Re(ρ)}{∂f}\frac{∂^{2}Im(ρ)}{∂f^{2}}<\frac{∂Im(ρ)}{∂f}\frac{∂^{2}Re(ρ)}{∂f^{2}}[/itex]
or, equivalently,
[itex]\frac{∂}{∂f}\left[\frac{\frac{∂Im(ρ)}{∂f}}{\frac{∂Re(ρ)}{∂f}}\right]<0[/itex]→[itex]\frac{∂}{∂f}\left(\frac{∂Im(ρ)}{∂Re(ρ)}\right)<0[/itex]
The same would apply to the complex impedance Z=R+j*X, (or admittance), i.e., [itex]\frac{∂R}{∂f}\frac{∂^{2}X}{∂f^{2}}<\frac{∂X}{∂f}\frac{∂^{2}R}{∂f^{2}}[/itex] and [itex]\frac{∂}{∂f}\left(\frac{∂X}{∂R}\right)<0[/itex]
Is all this right?
Do you know any theorem, property of LTI causal passive systems, energy considerations from which one may conclude this? Kramer-Kronig relations or Hilbert transform?
I would appreciate your help on this.
Last edited: