- #1
Stealth849
- 38
- 0
Hi, I'm new to the forum, starting off with some rotational stuff that I am not grasping well...
I have diagrams for each question too, which i feel are vital to understanding the questions
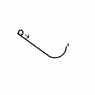
A spherical ball bearing 0.025m in diameter, rolls without slipping down an inclined track which becomes circular and ends at point P where the track becomes vertical. Point P is 0.65m below the level from which the ball bearing was released from rest.
a) what angular velocity (in r.p.m.) will the ball bearing have when it leaves the track at point P?
b) how high will it rise above point P?
conservation of energy, I = 0.5*m*r^2, v = Rω
I'm not sure how to deal with the fact that I don't know the total height of the ball bearing - only the top half. So I can't really set one of the potential energy terms to zero... I tried working out a formula using conservation of energy:
gh = 0.5*v^2 + 0.2*r^2*ω^2 + gh_p
v = Rω
gh = 0.5*r^2*ω^2 + 0.2*r^2*ω^2 + gh_p
gh = 0.7*r^2*ω^2 + gh_p
ω = sqrt((10g(h - h_p))/7r^2)
with that though, providing it is correct at all... I can't get a quantitative value without knowing the total initial height. am i on the right track at all?
for part b, I'm not sure whether or not to consider this as completely conserved, which would mean it rises to it's initial height after point P, but I can't see where I'd go otherwise..
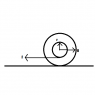
A string is wrapped around the small cylinder. If the string is pulled horizontally with a force F, what is the acceleration of the cylinder?
r = 0.03m, R = 0.05m, F = 0.1N, m = 1kg
τ = r x F / τ = rFsin(θ)
τ = I*α
a = r*α
I started by finding the torque of the smaller cylinder using rFsin(θ)
0.03m* 0.1N* sin(90) = 0.003mN
Then using τ = I*α, where I = mr^2/2, I solved for alpha, since the torque on the small cylinder should be the total torque on the system...
α = 2τ/MR^2
2(0.003)/(0.05)^2 = 2.4rad/s^2
using a = R*α, i found an acceleration of 0.12m/s^2
Hopefully I'm doing these questions somewhat right, or am on the right track. Thanks for your time.
I have diagrams for each question too, which i feel are vital to understanding the questions
Homework Statement
A spherical ball bearing 0.025m in diameter, rolls without slipping down an inclined track which becomes circular and ends at point P where the track becomes vertical. Point P is 0.65m below the level from which the ball bearing was released from rest.
a) what angular velocity (in r.p.m.) will the ball bearing have when it leaves the track at point P?
b) how high will it rise above point P?
Homework Equations
conservation of energy, I = 0.5*m*r^2, v = Rω
The Attempt at a Solution
I'm not sure how to deal with the fact that I don't know the total height of the ball bearing - only the top half. So I can't really set one of the potential energy terms to zero... I tried working out a formula using conservation of energy:
gh = 0.5*v^2 + 0.2*r^2*ω^2 + gh_p
v = Rω
gh = 0.5*r^2*ω^2 + 0.2*r^2*ω^2 + gh_p
gh = 0.7*r^2*ω^2 + gh_p
ω = sqrt((10g(h - h_p))/7r^2)
with that though, providing it is correct at all... I can't get a quantitative value without knowing the total initial height. am i on the right track at all?
for part b, I'm not sure whether or not to consider this as completely conserved, which would mean it rises to it's initial height after point P, but I can't see where I'd go otherwise..
Homework Statement
A string is wrapped around the small cylinder. If the string is pulled horizontally with a force F, what is the acceleration of the cylinder?
r = 0.03m, R = 0.05m, F = 0.1N, m = 1kg
Homework Equations
τ = r x F / τ = rFsin(θ)
τ = I*α
a = r*α
The Attempt at a Solution
I started by finding the torque of the smaller cylinder using rFsin(θ)
0.03m* 0.1N* sin(90) = 0.003mN
Then using τ = I*α, where I = mr^2/2, I solved for alpha, since the torque on the small cylinder should be the total torque on the system...
α = 2τ/MR^2
2(0.003)/(0.05)^2 = 2.4rad/s^2
using a = R*α, i found an acceleration of 0.12m/s^2
Hopefully I'm doing these questions somewhat right, or am on the right track. Thanks for your time.