- #1
Vibhor
- 971
- 40
Homework Statement
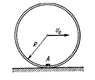
A small body A is fixed to the inside of a thin rigid hoop of radius R and mass equal to that of the body A. The hoop rolls without slipping over a horizontal plane; at the moments when the body A gets into the lower position, the center of the hoop moves with velocity v0. At what values of v0 will the hoop move without bouncing?
Ans : √(8gR)
Homework Equations
The Attempt at a Solution
The center of mass is located at a distance R/2 from the center of the hoop.CM rotates in a circle of radius R/2 about the center of hoop.
The forces acting on the system(hoop+mass A) are normal from the surface and weight 2mg.
Applying ∑F = ma , N-2mg=2may ,where ay is the acceleration of the CM in vertical direction.
The hoop will move without bouncing if normal force due to the surface is not zero.
I am not able to make any progress .Please help me .
Attachments
Last edited: