Rotational Energy, ball on a loop

[bigguccisosa]

Homework Statement

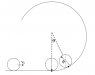
Imagine a ball with moment of inertia I_{cm} = \beta MR^2 encountering a circular loop of radius R_0 > R after rolling on a level surface at a speed of v_0. Assume that the ball does not slip. Attached a diagram.
A) What is the minimum value of v_0 required for the ball to reach the point where the track becomes vertical?
B) What is the minimum value of v_0 required for the ball to reach the top of the track?

Homework Equations

Rotational Kinetic Energy = T = \frac{1}{2}Mv^2 + \frac{1}{2}I\omega^2
Total Mechanical Energy = T + U

The Attempt at a Solution

So I thought I might use energy conservation here, for part A), if the ground is taken to be zero potential energy, there is no speed when the ball just reaches the vertical track, so kinetic energy is zero, and the ball is R_0 above the ground. The centre of the ball starts R above the ground.
MgR_0 = \frac{1}{2}Mv_0^2 + \frac{1}{2}I \omega^2 + MgR
Replacing I and omega, MgR_0 = \frac{1}{2}Mv_0^2 + \frac{1}{2}\beta MR^2\frac{v_0^2}{R^2} + MgR
MgR_0 - MgR = \frac{1}{2}Mv_0^2 + \frac{1}{2}\beta MR^2\frac{v_0^2}{R^2}
Mg(R_0-R) = \frac{1}{2}Mv_0^2(1+\beta)
solving for speed v_0 = \sqrt{\frac{2g(R_0-R)}{1+\beta}}

For part B) did the same thing except put the height at the top of the track to be 2R_0-R,
and I solved for speed again and got v_0 = 2\sqrt{\frac{g(R_0-R)}{1+\beta}}

Is there a way to check if these are correct?, I'm unsure about how I calculated the potential energy, using the centre of mass of the ball? One of my classmates got v_0 = \sqrt{2gr_0 (1+\beta)} for part A instead?

 

[haruspex]

I agree with your answer for part A.
In part B, you are again assuming no KE at the top. If so, would what would happen next? Does that overall trajectory seem right?

 

[bigguccisosa]

Hi haruspex, I assumed zero KE at the top because the question asked for minimum velocity required to reach the top. I suppose right afterward, if there was no kinetic energy at the top, the ball would then drop in a straight line down? I don't see if there is a problem with this

 

[haruspex]

Hi haruspex, I assumed zero KE at the top because the question asked for minimum velocity required to reach the top. I suppose right afterward, if there was no kinetic energy at the top, the ball would then drop in a straight line down? I don't see if there is a problem with this

You wouldn't be surprised to see a ball do that, roll all the way to the top of the arc then drop vertically?
Think about the forces acting on the ball when it is near the top, so, according to your scheme, only moving slowly.

 

[bigguccisosa]

Oh man, I just pictured that and that is quite odd . On second thought, the ball should leave the track but still be moving "forwards", correct? It just doesn't have the velocity to stay on the track anymore. So I suppose the new assumption is that at the top, the kinetic energy must be such that the centripetal force just equals gravity?

 

[haruspex]

Oh man, I just pictured that and that is quite odd . On second thought, the ball should leave the track but still be moving "forwards", correct? It just doesn't have the velocity to stay on the track anymore. So I suppose the new assumption is that at the top, the kinetic energy must be such that the centripetal force just equals gravity?

Bingo.