- #1
naji0044
- 7
- 0
- Homework Statement
- Finding the rotational inertia
- Relevant Equations
- I=∑m*r^2
Problem Statement: Finding the rotational inertia
Relevant Equations: I=∑m*r^2
A rigid body of 2 massive globes with homogenous mass distribution and a thin rod is connecting the 2 globes. The globes has radius R1 = 0.18 m and R2 =0.28 m and masses m1=193 kg and m2=726 kg. The thin rod has the mass ms=10kg and the length L=0.88 m. THe body can rotate frictionless around the rotation axis in the middle of the thin rod.
a) Calculate the the body's overall inertiamoment and show that the inertiamoment is I=476 kgm^2
my calculations are m1*(1/2*L+r1)^2+m2*(1/2*L+r2)^2 and i doubt if this is even correct and can't tell how the inertiamoment of the rod would look. Ignore the F(force)
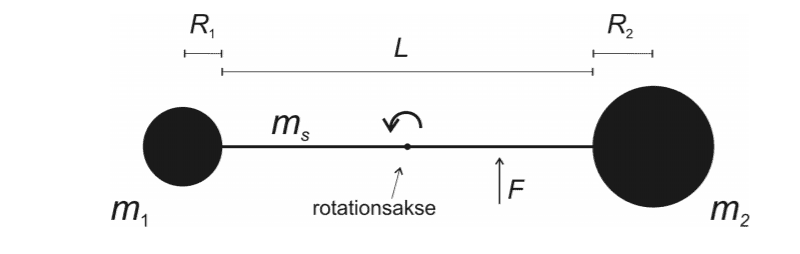
Relevant Equations: I=∑m*r^2
A rigid body of 2 massive globes with homogenous mass distribution and a thin rod is connecting the 2 globes. The globes has radius R1 = 0.18 m and R2 =0.28 m and masses m1=193 kg and m2=726 kg. The thin rod has the mass ms=10kg and the length L=0.88 m. THe body can rotate frictionless around the rotation axis in the middle of the thin rod.
a) Calculate the the body's overall inertiamoment and show that the inertiamoment is I=476 kgm^2
my calculations are m1*(1/2*L+r1)^2+m2*(1/2*L+r2)^2 and i doubt if this is even correct and can't tell how the inertiamoment of the rod would look. Ignore the F(force)