Rotational Inertias of Different Shapes

[Meta14]

Sorry, this isn't a question from a book or something, but I wasn't sure where else to put this. Is there a convenient way of memorizing or deriving the following?:

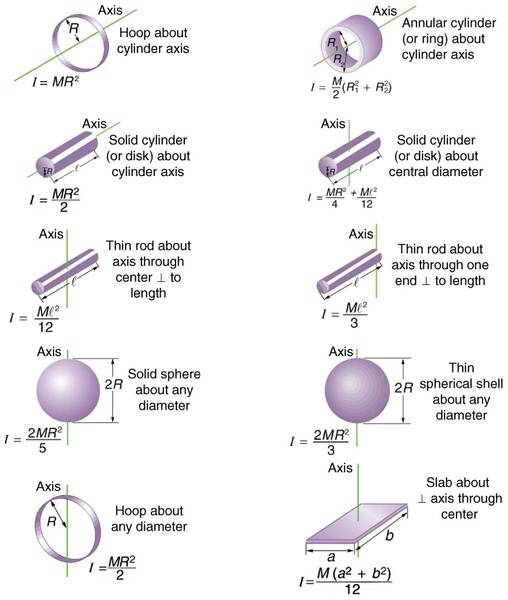
I have an exam in a week and I thought I might as well try asking before making flashcards.

 

[hjelmgart]

Well, you can see, how the inertia is defined by an integral here:
http://hyperphysics.phy-astr.gsu.edu/hbase/mi.html

So basically, it's just about putting up the correct integral and solve it. I did not, however, ever need to actually derive one of them through any of my physics studies. If your teacher hasn't done it, I doubt you will be asked to. If you cannot use books or anything for the exam, I would believe, that an equation for the inertia needed for the specific body will surely be given.