- #1
CStudent
- 15
- 0
Hey.
I have the following question to solve:
* Given a matrix A that is size m x n and m>n.
Let R be the RREF that we get by Gaussian elimination of A.
Prove that the system equation Ax=0 has only one solution iff in every column of R there is a leading element.
I have some answer of intuition so I'm not really sure,
Let's assume that we had R with some free variable, and we know(?) that any free variable has a degree of freedom which means that it yields infinite number of solutions.
Now, I am not sure again about the establishment of this proof and to what extent it's accurate. Moreover, I am not if it proves the point of iff (equivalence).
Another similar question, but I have no idea what it means:
* Given a matrix A that is size m x n and m>n.
Let R be the RREF that we get by gaussian elimination of A.
Prove that for every
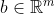 the system equation Ax=b has a solution iff R doesn't have rows of zeros.
the system equation Ax=b has a solution iff R doesn't have rows of zeros.
Thank you!
I have the following question to solve:
* Given a matrix A that is size m x n and m>n.
Let R be the RREF that we get by Gaussian elimination of A.
Prove that the system equation Ax=0 has only one solution iff in every column of R there is a leading element.
I have some answer of intuition so I'm not really sure,
Let's assume that we had R with some free variable, and we know(?) that any free variable has a degree of freedom which means that it yields infinite number of solutions.
Now, I am not sure again about the establishment of this proof and to what extent it's accurate. Moreover, I am not if it proves the point of iff (equivalence).
Another similar question, but I have no idea what it means:
* Given a matrix A that is size m x n and m>n.
Let R be the RREF that we get by gaussian elimination of A.
Prove that for every
Thank you!
Last edited: