Roxy's question at Yahoo Answers regarding finding the area between two curves

[MarkFL]

Here is the question:

Calculus finding the area between the curves on the interval?

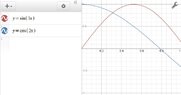
find the area between the curves on the interval [0,1]. y=sin3x and y=cos2x

please show me the steps thank you !

I have posted a link there to this thread so the OP can view my work.

 

[MarkFL]

Hello Roxy,

The area in question can be found with:

\(\displaystyle A=\int_0^1 \left|\sin(3x)-\cos(2x) \right|\,dx\)

Here is a graph of the two curves over the given interval:

View attachment 2239

We need to find where the two curves intersect so that we may split the integral into two integral where the integrand of each contains the upper curve minus the lower curve. So, equating the two curves, we have:

\(\displaystyle \sin(3x)=\cos(2x)\)

Applying a triple-angle identity for sine on the left and a double-angle identity for cosine on the right, we have:

\(\displaystyle 3\sin(x)-4\sin^3(x)=1-2\sin^2(x)\)

We may then arrange this as:

\(\displaystyle 4\sin^3(x)-2\sin^2(x)-3\sin(x)+1=0\)

Factor:

\(\displaystyle \left(\sin(x)-1 \right)\left(4\sin^2(x)+2\sin(x)+1 \right)=0\)

The only root that results in $x$ being in the given interval comes from:

\(\displaystyle \sin(x)=\frac{-1+\sqrt{5}}{4}\implies x=\frac{\pi}{10}\)

And so, we may state:

\(\displaystyle A=\int_0^{\frac{\pi}{10}} \cos(2x)-\sin(3x)\,dx+\int_{\frac{\pi}{10}}^1 \sin(3x)-\cos(2x)\,dx\)

Applying the FTOC, we obtain:

\(\displaystyle A=\left[\frac{1}{2}\sin(2x)+\frac{1}{3}\cos(3x) \right]_0^{\frac{\pi}{10}}-\left[\frac{1}{3}\cos(3x)+\frac{1}{2}\sin(2x) \right]_{\frac{\pi}{10}}^1\)

\(\displaystyle A=\frac{1}{2}\sin\left(\frac{\pi}{5} \right)+\frac{1}{3}\cos\left(\frac{3\pi}{10} \right)-\frac{1}{3}-\frac{1}{3}\cos(3)-\frac{1}{2}\sin(2)+ \frac{1}{3}\cos\left(\frac{3\pi}{10} \right)+\frac{1}{2}\sin\left(\frac{\pi}{5} \right)\)

Combine like terms:

\(\displaystyle A=\sin\left(\frac{\pi}{5} \right)+\frac{2}{3}\cos\left(\frac{3\pi}{10} \right)-\frac{1}{3}-\frac{1}{3}\cos(3)-\frac{1}{2}\sin(2)\)

\(\displaystyle A=\frac{1}{12}\left(5\sqrt{2\left(5-\sqrt{5} \right)}-\left(6\sin(2)+4\cos(3)+4 \right) \right)\approx0.521657539274763\)