- #36
BvU
Science Advisor
Homework Helper
- 16,126
- 4,882
Coming back to
 ...
...
(and the ##\mathcal O## is also on edge -- I personally would take 0.5E-7 or even 0.5E-8 ...
- - - -
When I finally got something to work (see #18) the results allow guestimating the 'correct digits':
(step size, ##x_0## for bounce 1,2,3)
5.0e-5 ##\qquad## -0.353496957103320 ##\qquad## 0.433854331752568 ##\qquad## 0.913422978195822
5.0e-4 ##\qquad## -0.353496957103362 ##\qquad## 0.433854331752487 ##\qquad## 0.913422978195706
5.0e-3 ##\qquad## -0.353496957539166 ##\qquad## 0.433854330903075 ##\qquad## 0.913422976982109
2.5e-2 ##\qquad## -0.353497244187681 ##\qquad## 0.433853767233959 ##\qquad## 0.913422170776847
So a step size of 5e-3 looks like a safe choice with 8+ significant digits.
- - - - -
Step size 5e-4 gave me local truncation errors of machine precision (#32), so I tried again with step size 5e-3.
Forget about the bouncing, just integrate from 0 to t=0.3 in 60 steps.
At each of these points ##n## I also do a two step RK4 with step size 2.5e-3.
That gives me a vector ##(t_{n+1},x^*,y^*,\dot x^*, \dot y^*)\quad ##
So I have (in MIT (7.17 notation) ##y(x+h)## and ##y(x+h/2+h/2)##.
And therefore an estimate of the local truncation error for both horizontal position: ##x_{n+1} - x^*## and vertical position: ##y_{n+1} - y^*##.
In pictures:
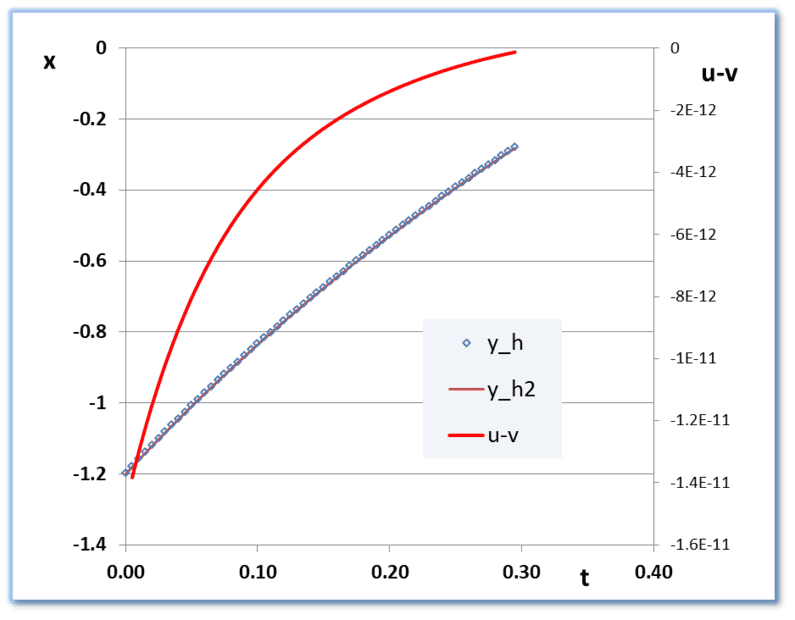
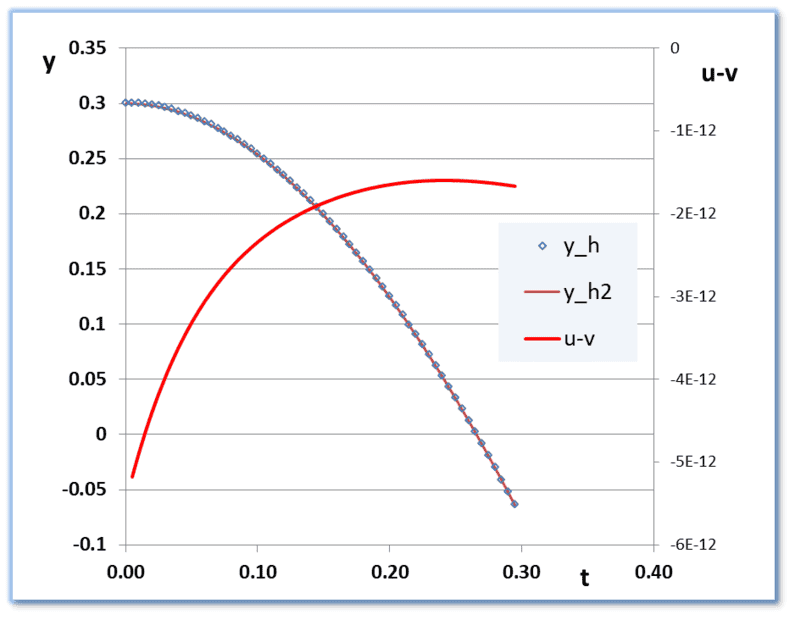
x(t) is almost a straight line and y(t) is almost a parabola .
.
The red lines show the local truncation error estimates (I dubbed them 'u-v' somehow) All negative.
Even a pessimistic global error estimate (just add absolute values) yields a maximum uncertainty in ##x## and ##y## after 54 steps of
about 2e-10. Consistent with the 9 significant digits above.
With the bouncing back in: two or three steps to find the exact moment are enough; the accumulated error for the first bounce will still be 2e-10 and the second and third a bit more. But no reason at all to halve step sizes.
I can't answer 'where in the "solution" matrix the new y is stored?'
In the fortran I added an array for the ##+h/2+h/2## results. In your matlab that would be a second solution matrix, I suppose.
I see pbuk added two posts. Will look at them later.
##\ ##
andbremenfallturm said:I've now changed it to 0.00005. ##\mathcal O## is 0.5⋅10−6, which is the highest error tolerated by the assignment.
when you reportbremenfallturm said:"The answers should have at least 6-8 correct digits, somewhat depending on question" (yes, this is what the assignment says)
Where I'm afraid I have to remark that this doesn't satisfy the 'at least 6-8 correct digits'bremenfallturm said:x-values for comparison for fun, here's what I get using the initial conditions given in the top post: (for the three bounces before x=1.2)
-3.53496e-01 4.3385e-01 9.1342e-01
(and the ##\mathcal O## is also on edge -- I personally would take 0.5E-7 or even 0.5E-8 ...
- - - -
When I finally got something to work (see #18) the results allow guestimating the 'correct digits':
(step size, ##x_0## for bounce 1,2,3)
5.0e-5 ##\qquad## -0.353496957103320 ##\qquad## 0.433854331752568 ##\qquad## 0.913422978195822
5.0e-4 ##\qquad## -0.353496957103362 ##\qquad## 0.433854331752487 ##\qquad## 0.913422978195706
5.0e-3 ##\qquad## -0.353496957539166 ##\qquad## 0.433854330903075 ##\qquad## 0.913422976982109
2.5e-2 ##\qquad## -0.353497244187681 ##\qquad## 0.433853767233959 ##\qquad## 0.913422170776847
So a step size of 5e-3 looks like a safe choice with 8+ significant digits.
- - - - -
Step size 5e-4 gave me local truncation errors of machine precision (#32), so I tried again with step size 5e-3.
Forget about the bouncing, just integrate from 0 to t=0.3 in 60 steps.
Gives me 61 vectors ##(t_n,x_n,y_n,\dot x_n, \dot y_n)\quad ## n = 0 to 60bremenfallturm said:What y do you compare to do that? And how do you find out where in the "solution" matrix the new y is stored?
At each of these points ##n## I also do a two step RK4 with step size 2.5e-3.
That gives me a vector ##(t_{n+1},x^*,y^*,\dot x^*, \dot y^*)\quad ##
So I have (in MIT (7.17 notation) ##y(x+h)## and ##y(x+h/2+h/2)##.
And therefore an estimate of the local truncation error for both horizontal position: ##x_{n+1} - x^*## and vertical position: ##y_{n+1} - y^*##.
In pictures:
x(t) is almost a straight line and y(t) is almost a parabola
The red lines show the local truncation error estimates (I dubbed them 'u-v' somehow) All negative.
Even a pessimistic global error estimate (just add absolute values) yields a maximum uncertainty in ##x## and ##y## after 54 steps of
about 2e-10. Consistent with the 9 significant digits above.
With the bouncing back in: two or three steps to find the exact moment are enough; the accumulated error for the first bounce will still be 2e-10 and the second and third a bit more. But no reason at all to halve step sizes.
I can't answer 'where in the "solution" matrix the new y is stored?'
In the fortran I added an array for the ##+h/2+h/2## results. In your matlab that would be a second solution matrix, I suppose.
I see pbuk added two posts. Will look at them later.
##\ ##
 . Don't have MatLab, so downloaded Octave and fought my way in. Both horrible and fascinating at the same time (for a 1980's Fortran 77 'expert'). Results identical to what I already had in all digits -- including the error estimates and the bouncing points
. Don't have MatLab, so downloaded Octave and fought my way in. Both horrible and fascinating at the same time (for a 1980's Fortran 77 'expert'). Results identical to what I already had in all digits -- including the error estimates and the bouncing points