- #1
M_Abubakr
- 10
- 1
- TL;DR Summary
- Applying Periodic Boundary Conditions on a Composite REV.
Hi
I have a project regarding micromechanics of composites. I'm starting my analysis on the Fiber Matrix RVE. Right now I'm trying to find the natural frequency of the unit cell. The Unit cell has some unique geometry which I will keep on changing to see how natural frequency changes.
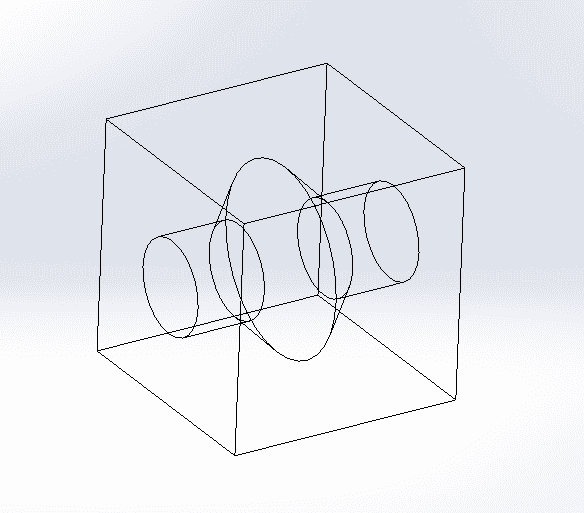

I have to apply infinite periodic boundary on this unit cell, Up-down, left-right, front-back. I want to know how to do it because I'm running out of time and can't find any solutions to it. The mesh on all opposite sides of the unit cell is same since there are no double lines and the structure itself is symmetric. I know this is easier to do in Abaqus but I'm very unfamiliar with it and have wasted days on it. Can anyone please explain step by step what to do? I would really appreciate it.
I have a project regarding micromechanics of composites. I'm starting my analysis on the Fiber Matrix RVE. Right now I'm trying to find the natural frequency of the unit cell. The Unit cell has some unique geometry which I will keep on changing to see how natural frequency changes.
I have to apply infinite periodic boundary on this unit cell, Up-down, left-right, front-back. I want to know how to do it because I'm running out of time and can't find any solutions to it. The mesh on all opposite sides of the unit cell is same since there are no double lines and the structure itself is symmetric. I know this is easier to do in Abaqus but I'm very unfamiliar with it and have wasted days on it. Can anyone please explain step by step what to do? I would really appreciate it.
Last edited by a moderator: