S-domain transformations (Laplace)

[dwn]

Homework Statement

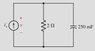
Image attached.

Homework Equations

S-domain transformations

The Attempt at a Solution

Solving this using mesh analysis.
I1 is straightforward : V = I1R I1 = 1.8∠75° / 2 = 0.9∠75°

I2 I'm having a little trouble with.

i = C dv/dt = C*V*s

.250(1.8∠75°)(-2+j1.5)
.250(4.5∠38.13°) after converting s to polar coordinates.

ans: i(t) = 0.52e^-2tcos(1.5t + 129.4 °)

 

[donpacino]

I am having trouble following what you did.
where did you get 1.8 angle 75?
What is the value of IS?
what are you trying to solve for?
Is the circuit in steady state?

 

[dwn]

My apologies. That is the voltage across circuit -- it is given in the problem statement. I was solving for I1 = V/R.

I don't think steady state is relevant to this question. Once we solve for i across each component in the circuit, I = I1 + I2.

I attached the problem in the images. We're supposed to solve for i...?

 

[donpacino]

I did not see the problem statement

EDIT: Did not realize it was a complex frequency. This implies that the system is in transient and not steady state. do not take note of the underlined section

That being said you skipped a few steps so its hard to tell what you did. I can tell you that your answer is incorrect. I know that because of the decaying function (e^-2t). That kind of respond only appears in transient circuits, not steady state circuits.

You need to determine Is, which is Ir+Ic (you called them I1 and I2). We know this by doing a kcl at the top node.

When you are doing problems such as these it makes everything a lot easier to write out your final expression symbolically.

Is=I1+I2
I1=V/R
I2=V*C*S

Is=V*(1/R+C*S)
...