guyvsdcsniper
- 264
- 37
- Homework Statement
- σ 1 and σ 2 are pasted to 2 spherical dielectric surfaces w/ radius r and 2R
2.)Calc. E when r<R and r>2R
3.)Calc E when R<r<2R
- Relevant Equations
- Dipole Potential
I have found the total dipole moment of for this problem but am having trouble finding the electric field.
I believe my electric field when r>2R ( I mistakenly wrote it as r<2R on my work, but it is the E with a coefficient of 2/3) is correct as it fits the equation:
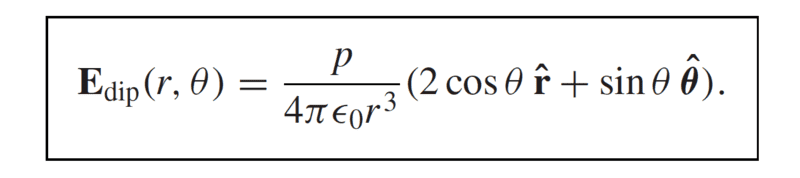 .
.
I don't believe this formula applies inside the sphere though, just based off experience with other problems because with other problems, I don't get that 2cosθ +sinθ. Which is making me second guess my E for r<R. Mathematically it seems correct but I feel I may be missing something fundamental.
Do my E.F. for r<R and r>2R seem correct?
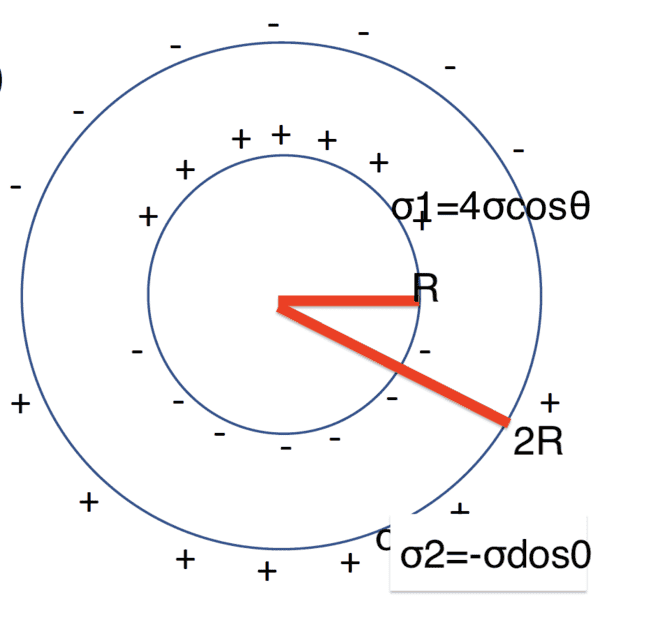
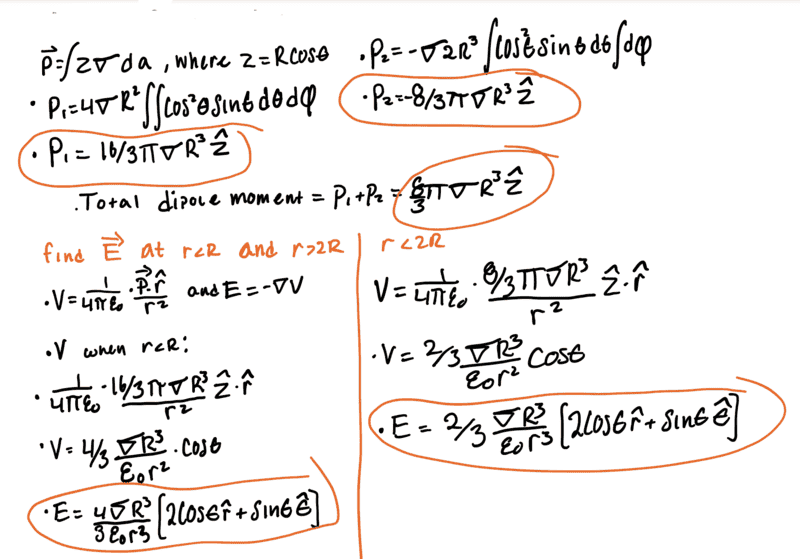
I believe my electric field when r>2R ( I mistakenly wrote it as r<2R on my work, but it is the E with a coefficient of 2/3) is correct as it fits the equation:
I don't believe this formula applies inside the sphere though, just based off experience with other problems because with other problems, I don't get that 2cosθ +sinθ. Which is making me second guess my E for r<R. Mathematically it seems correct but I feel I may be missing something fundamental.
Do my E.F. for r<R and r>2R seem correct?