#s of Combinations and Permutations of lines?

[Laubarr]

Hello All,

See picture below:

There exist an infinite plane with infinite number of dots. For sake of argument, let's assume they are 1 inch away from each other.

However, below(on your far left) you can see 3 lines already made. The last line is the yellow one.
What you see on the left, are all combinations of possible moves. Move is defined as structure of lines until you reach an empty dot.
Thus, there are 6 combinations of single line(on top). While on bottom you see 10 combinations. 5 of them moves with 2 lines, and 5 with 3 lines.
Total # of combinations is 16.

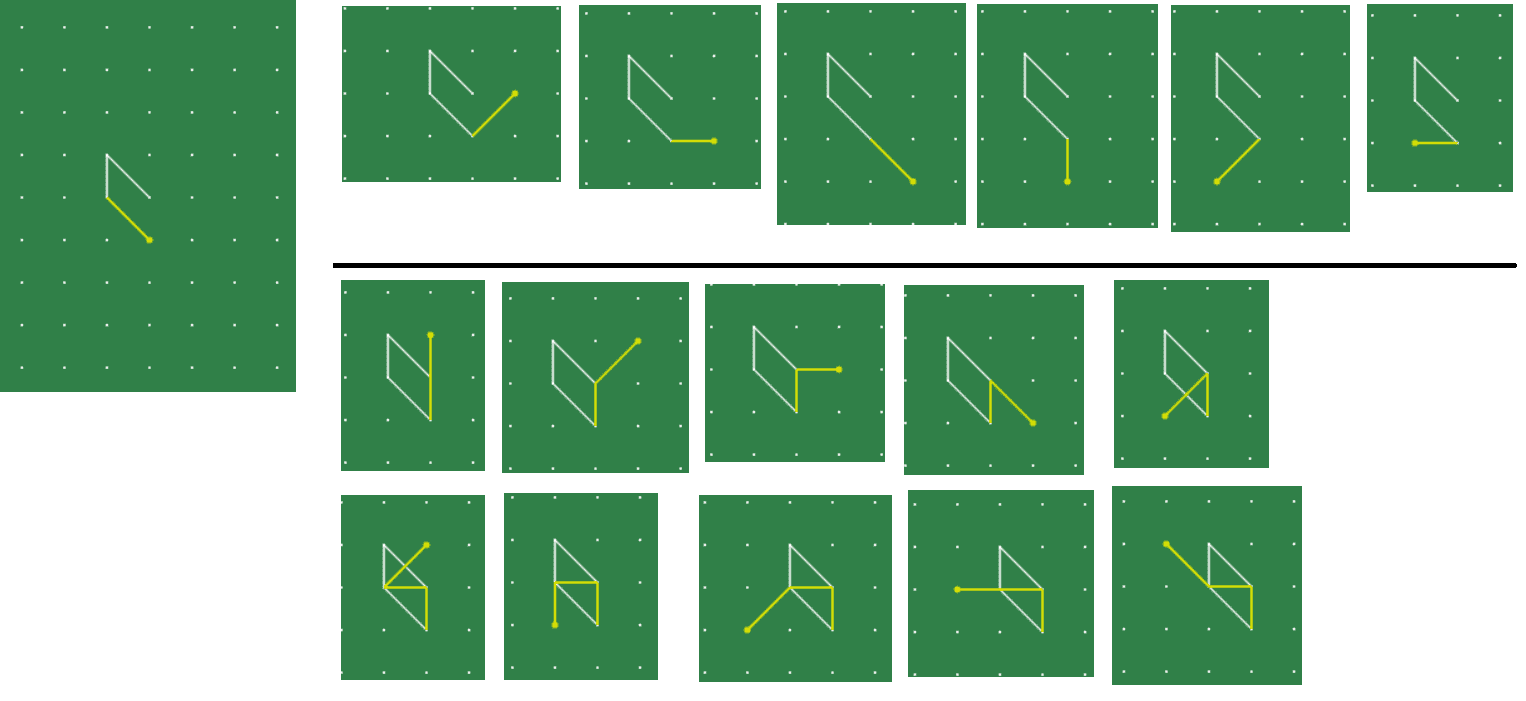
So far so good?
Well the basic unsolved question are:
* Does formula exist to calculate total number of combinations(16 in this case) just by looking at the initial graph of 3 lines?
** Does formula exist to show the breakdown of all combinations (6 for single line, 5 for 2 lines, 5 for 3 lines?
*** is 16 the biggest number of combinations that you can make from 3 line starting configuration? For instance: Try to calculate # of combinations (1 lines, 2 lines, 3 lines) from this initial variation:

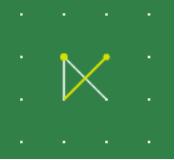
To not spoil the fun, i will just say there is more than 16. So is this the best solution? How we can prove that this is the best we can do? Obviously we can prove that just by doing all 3 line configurations by hand, but what if we take it to next level? What's the best 4 line configuration and how many combinations it has? How about 5,6.7...(n) ? The tree expands quite rapidly, and also few things need to be explained:

Combinations vs Permutations:

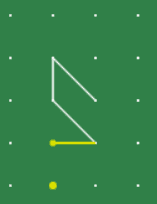
Above, there are 4 lines as starting configuration. In this case, there are 36 combinations OR 41 permutations. The reason is because you can go from A > B > C > D or C > B > A > D. Once again, is the a formula to calculate combinations (36) and Permutation(41) from any starting configuration?

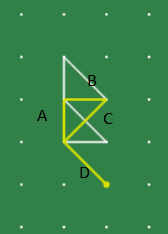
Notation + Final info to consider:

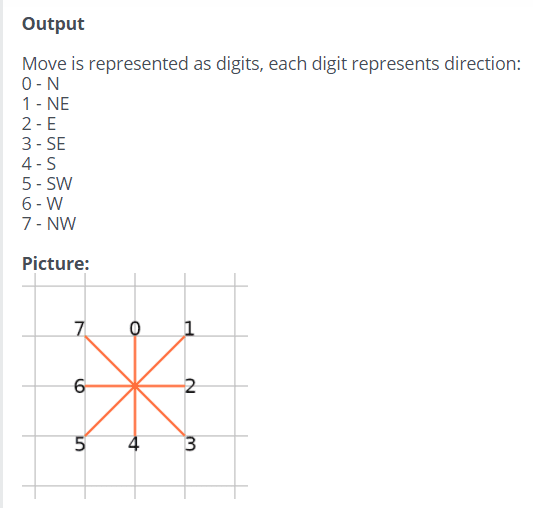
Using above notation, you can notice that each configuration is unique and might have different #s of combinations and or permutations. For example:

Anyone with any input, either mechanical or potentially writing a code to get the answers How many combinations/Permutations for each variation with up to 10 lines as a starting configuation, would be greatly appreciated. If your program can handle bigger starting configurations, that's even better!

Thank You and enjoy! :)

 

[jvicens]

Hello there,

I can definitely provide some insights and potential solutions to the questions posed in the forum post.

Firstly, to answer the question about the formula for calculating the total number of combinations, it is possible to do so using a mathematical concept known as combinations with repetition. In this case, the number of combinations can be calculated using the formula n^r, where n represents the total number of distinct elements (in this case, lines) and r represents the number of elements in each combination. So for the example given, where there are 3 lines and each combination consists of 2 lines, the formula would be 3^2 = 9 combinations. This can be extended to any number of lines and combination sizes.

To show the breakdown of all combinations, we can use another mathematical concept called binomial coefficients. This allows us to calculate the number of ways to choose r elements from a set of n elements. In the example given, where there are 3 lines and each combination consists of 2 lines, the formula would be (3 choose 2) = 3 combinations. This can also be extended to any number of lines and combination sizes.

Moving on to the question about whether 16 is the biggest number of combinations for a starting configuration of 3 lines, the answer is no. As mentioned in the post, there are more than 16 combinations for this starting configuration. To prove this, we can use the formula mentioned earlier (n^r). For 3 lines and combinations of 2 lines, the maximum number of combinations would be 3^2 = 9. So there are definitely more than 9 combinations in this case.

As for the question about the best 4 line configuration and the number of combinations it has, the same concepts can be applied. Using the formula n^r, we can calculate that there are 4^2 = 16 combinations for a starting configuration of 4 lines with combinations of 2 lines. This can also be extended to any number of lines and combination sizes.

To answer the question about combinations vs permutations, it is important to understand the difference between the two. Combinations refer to the number of ways to choose a subset of elements from a larger set, while permutations refer to the number of ways to arrange a set of elements in a specific order. In the example given, there are 36 combinations but 41 permutations because some combinations can be arranged in different orders to