-s2.9 parabola....vertex, open direction, increasing, decreasing, zeros

[karush]

What are intervals of which the function $g(t)=3t^2-5t+1$
a. find the vertex convert to vertex form $g(t)=a(t-h)^2-k$
\item $g(t)=3\left(t-\dfrac{5}{3}t+\left(\dfrac{5}{6}\right)^2\right)
+1-\dfrac{25}{12}
=3\left(t-\dfrac{5}{6}\right)^2-\dfrac{13}{12}$
b. the parabola opens up and the vertex is $\left(\dfrac{5}{6},-\dfrac{13}{12}\right)$
c. is decreasing or increasing
interval of increasing is $\left[\dfrac{5}{6}<x \right]$
and the interval of decreasing is $\left[x<\dfrac{5}{6}\right]

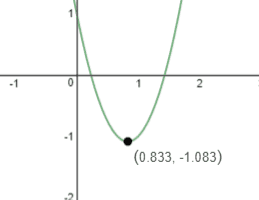
ok, hopefully this is correct
typos maybe

the parabola seens to be used a lot in speed problems

 

[Kansas Boy]

$g(t)=3t^2−5t+1= 3(t^2- \frac{5}{2}t)+ 1= 3(x^3- \frac{5}{2}x+ \frac{25}{16}- \frac{25}{16})+ 1$​

$g(t)= 3(x- \frac{5}{4})^2- \frac{75}{16}+ 1=$$ 3(x- \frac{5}{4})^2- \frac{59}{4}$.​

​

The vertex is at $\left(\frac{5}{4}, -\frac{59}{4}\right)$​

 

[karush]

ok just need to be more careful