karush
Gold Member
MHB
- 3,240
- 5
Given
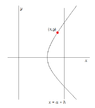
$$x_1^2 -y^2=a^2, \ \ x_2=a+h$$
Or
$$x_1=\sqrt{a^2+y^2}$$
Find
Volume about the $y$-axis
So...
$$\pi\int_{a}^{h} \left(x_2^2-x_1^2\right)\,dy$$
Actually I am clueless?!
$$x_1^2 -y^2=a^2, \ \ x_2=a+h$$
Or
$$x_1=\sqrt{a^2+y^2}$$
Find
Volume about the $y$-axis
So...
$$\pi\int_{a}^{h} \left(x_2^2-x_1^2\right)\,dy$$
Actually I am clueless?!