S8.02.4.58 type of discontinuity tikx with 1/sqrt(1-cos(2x))

[karush]

$\tiny{s8.2.4 58}$

desmos

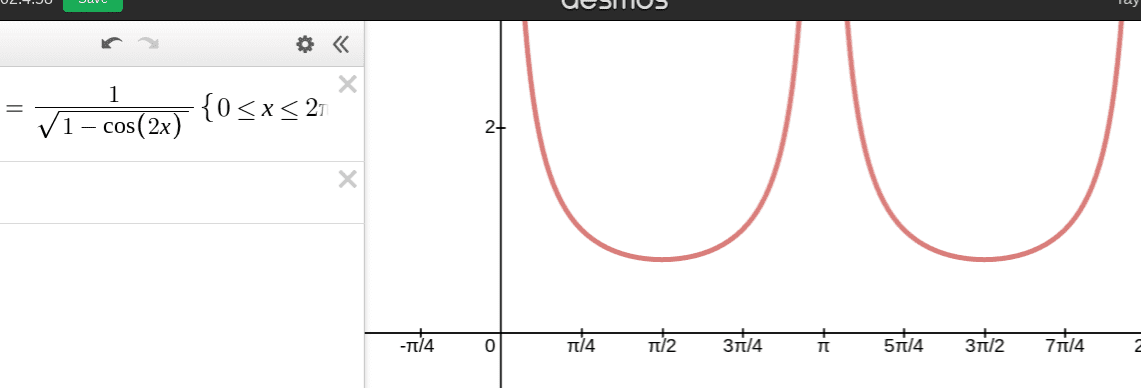
Let
$f(x)=\dfrac{1}{\sqrt{1-\cos{2x}}}$
(a) Graph $f$ What type of discontinuity does it appear to have at 0?\\
(b) Calculate the left and right limits of $f$ at 0. \\
Do these valuesn' confirm your answer to part (a)?

doesn't the limit going to 0 infinity both + and -

what is the tikx plot code for
$\dfrac{1}{\sqrt{1-\cos{2x}}}$ {1 / sqrt(x)} is as far as I gotalso what plotted in Overleaf didn't preview here

 

[HOI]

It's not clear to me what you are asking. What "types" of discontinuity are there? How is each defined?

Do you know what "left" and "right" limits are? (Since they ask about "left" and "right" of x= 0 you might want your graph to include some negative values of x.