- #1
hxtasy
- 112
- 1
Ok this is a pretty simple concept and in the electronics field I use it on a monthly basis, I can do it but I do not understand how it works and It is bugging the crap out of me.
EXAMPLE: I have a pressure sensor, it reads pressure from 0 psi to .73 psi, and outputs a corresponding voltage from 2.996 volts to 5 volts, completely linear. If I know the min and max of the pressure in and the minimum and maximum units of the voltage out, I can calculate the all the points in between with a slope line equation.
Now when I do this I usually just use the my calculator [TI-86] and use simult, because it is easier IMO than using matrices, but mathematically the same.
Below is a picture of how I set it up in my calculator, and then me plotting the points in excel and having excel compute the linear equation. I have three questions:
1.) Every time I do these equations I do something different or i fail a dozen times before succeeding. What is the correct way to set this up, or what is a consistent way I can set it up?
2.)Why is excel's equation and mine different? The scaling factor differs by almost ten percent and the offset differs by 15 percent. This is not acceptable, but the problem is, in "real life" when I feed values to the pressure sensor, from random points in between min and max, the excel equation is more accurate then my equation. I would think Mine would be more accurate as I didn't round any decimal places.
3.) How would you do the matrix by hand? Would it be the same as doing a wronskian? I hate relying on the calculator.
Thanks guys. I think I posted this question in the past but I wasn't as specific and therefore didn't get a satisfying answer. Help Appreciated!
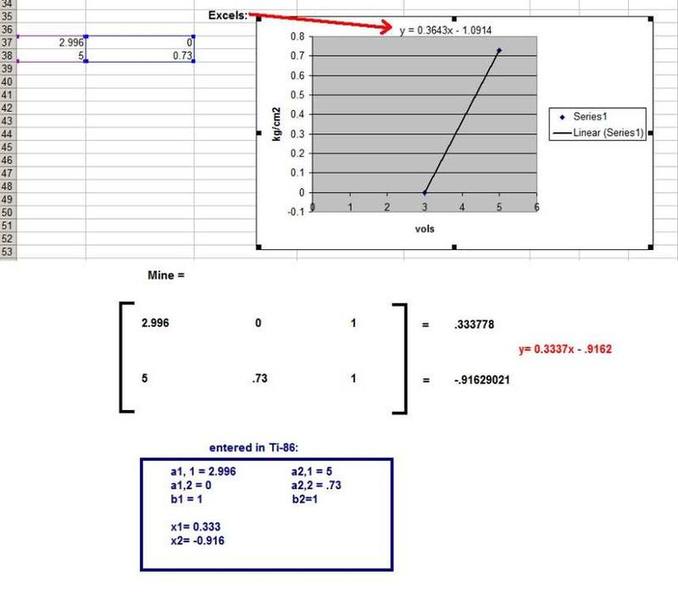
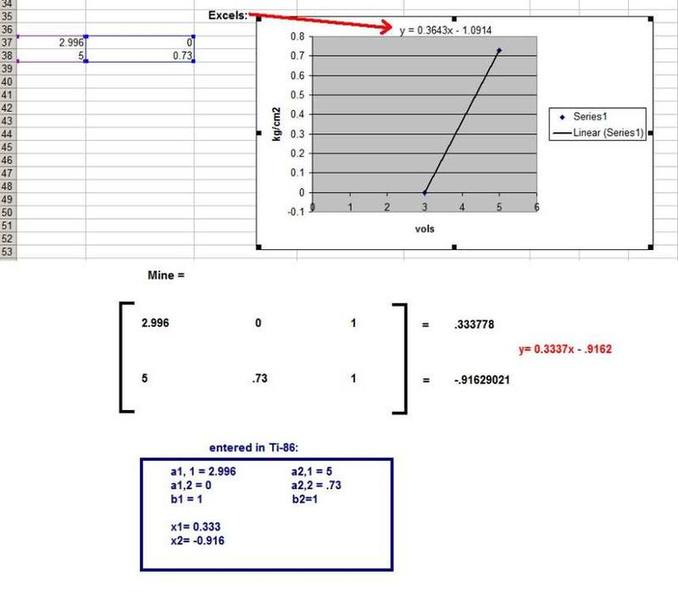
EXAMPLE: I have a pressure sensor, it reads pressure from 0 psi to .73 psi, and outputs a corresponding voltage from 2.996 volts to 5 volts, completely linear. If I know the min and max of the pressure in and the minimum and maximum units of the voltage out, I can calculate the all the points in between with a slope line equation.
Now when I do this I usually just use the my calculator [TI-86] and use simult, because it is easier IMO than using matrices, but mathematically the same.
Below is a picture of how I set it up in my calculator, and then me plotting the points in excel and having excel compute the linear equation. I have three questions:
1.) Every time I do these equations I do something different or i fail a dozen times before succeeding. What is the correct way to set this up, or what is a consistent way I can set it up?
2.)Why is excel's equation and mine different? The scaling factor differs by almost ten percent and the offset differs by 15 percent. This is not acceptable, but the problem is, in "real life" when I feed values to the pressure sensor, from random points in between min and max, the excel equation is more accurate then my equation. I would think Mine would be more accurate as I didn't round any decimal places.
3.) How would you do the matrix by hand? Would it be the same as doing a wronskian? I hate relying on the calculator.
Thanks guys. I think I posted this question in the past but I wasn't as specific and therefore didn't get a satisfying answer. Help Appreciated!
Last edited: