Schrodinger equation and Heisenberg equation of motion

[Josh1079]

My question is that how does the Schrödinger equation arise from the Heisenberg equation of motion in the quantum field formalism.

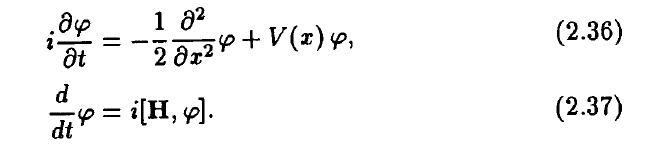
These are from Hatfield's book. So I'm having some difficulties to reproduce (2.36) by plugging (2.55) into (2.37) primarily because H is an integral.

Thanks!

 

[vanhees71]

Just use (2.54). Note that $\hat{H}$ is conserved in the Heisenberg picture, i.e., you can evaluate the integral at time $t$ (it doesn't depend on $t$ after all anyway). That's why you only need the canonical equal-time commutation relations (2.54).

 

[Josh1079]

Hi vanhees, great to see you again! Sorry I don't really follow you this time. I was also trying to use (2.54) and I guess I was stuck because I'm not familiar with an operator that is an integral.

So first of all, for the right side of (2.37) I'm not sure whether [H, \phi] = (\int dx \phi^* h \phi) \phi - \phi (\int dx \phi^* h \phi) or \int dx \phi^* h \phi \phi - \int \phi dx \phi^* h \phi, where h = -\frac{1}{2} \partial^2_x + V(x). Furthermore, when the operators are in the form h \phi \phi, is it equal to simply (h\phi) \phi or is it (h\phi)\phi + \phi (h\phi)?

 

[Josh1079]

Wait, I think I get something now.

Is it like this?

[H, \phi] = H\phi - \phi H = \int dx' \phi^*(x') h \phi(x') \phi(x) - \phi(x) \int dx' \phi^*(x') h \phi(x')
= \int dx' \phi^*(x') h \phi(x') \phi(x) - \int dx' \phi(x) \phi^*(x') h \phi(x')
the phi(x) can be taken inside the integral since it's independent of x', then by (2.54),
= \int dx' \phi^*(x') \phi(x) h \phi(x') - \int dx' \phi(x) \phi^*(x') h \phi(x') = \int \delta (x' - x) h \phi(x') dx' = h \phi(x)

Did I make any mistakes in the math?

 

[vanhees71]

I'm not familiar with your notation, and it's also good to write out the arguments. First of all you have
$$\hat{H}=\int_{\mathbb{R}} \mathrm{d} x \hat{\varphi}^*(t,x) \left (-\frac{1}{2} \Delta +V(x) \right) \hat{\varphi}(t,x).$$
Now $\hat{H}$ is not explicitly time dependent and that implies that it is conserved:
$$\frac{\mathrm{d}}{\mathrm{d} t} \hat{H}=[\hat{H},\hat{H}]+\partial_t \hat{H}=0.$$
That implies that you can use any $t$ in evaluating $\hat{H}$ since $\hat{H}$ doesn't depend on it. Now you have
$$[\hat{H},\hat{\varphi}(t,x)]=\int_{\mathbb{R}} \mathrm{d} x' \left [\hat{\varphi}^*(t,x') \left (-\frac{1}{2} \Delta' +V(x') \right) \hat{\varphi}(t,x'),\hat {\varphi}(t,x) \right ].$$
Now you can just use the equal-time commutator relations given in #1 to show (2.37). You also need the general formula
$$[\hat{A},\hat{B} \hat{C}]=[\hat{A},\hat{C}] \hat{B}+\hat{C} [\hat{A},\hat{B}],$$
valid for any three operators $\hat{A}$, $\hat{B}$, and $\hat{C}$.

It is allowed to use $t$ in the integral for $\hat{H}$ as the time argument of the fields since $\hat{H}$ doesn't depend on time as argued above, and that's why you can use the equal-time commutation relations to evaluate this commutator.