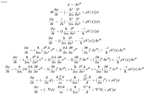lagrangman
- 13
- 2
I was playing with the Schrodinger equation and realized that it can be interpreted as a flow equation.
If we set $$ \psi = A e^{i \theta} $$
We can put the Schrodinger in the form ∂ψ∂t=(−∇ψ)⋅v+iEψ
If v=ℏθm and E=ℏ2m(−∇2AA+∇2θ)+ρV
I find this intuitive personally as it shows that the wavefunction flows. Is there any book that mentions this?
If we set $$ \psi = A e^{i \theta} $$
We can put the Schrodinger in the form ∂ψ∂t=(−∇ψ)⋅v+iEψ
If v=ℏθm and E=ℏ2m(−∇2AA+∇2θ)+ρV
I find this intuitive personally as it shows that the wavefunction flows. Is there any book that mentions this?
Attachments
Last edited: