- #1
mc172
- 3
- 0
I am designing a mating male and female threaded interface, where the nut is much weaker than the male thread. I need to be able to calculate a few things:
A. The maximum force (as preload) required to reach the yield point of the nut material.
B. The torque required to achieve the above.
The thread is 3/8-32 UNEF. The male part is either nickel plated brass or zinc, and the female part is injection moulded ABS.
The length of engagement is 0.15".
I have found a few equations, but different sources list different methods. What I have also found is nobody cares how much torque it requires to strip a thread, as the more common goal is to calculate how much preload is required to yield the shank.
First, I put the numbers into the FUTEK bolt torque calculator:

17in-lb sounds like a reasonable figure for maximum torque and near what I'd expect.
It would be nice if FUTEK displayed the equations they derived their answers from, but they don't.
So, here are some of the methods and equations I have found:
1. ATS = ∏nLeDsmin((1/2n) + 0.57735(Dsmin - Emax))
Where:
ATS = Shear area of root of nut threads (in2)
n = threads per inch = 32
Le = length of thread engagement = 0.15"
Dsmin = minimum OD of bolt threads = 0.375"
Enmax = maximum PD of nut = 0.3547"*
*Calculated using:
Enmax = dp = D - 0.64592p
Where p = 1/32
I confirmed the pitch diameter of 0.3547" from this chart.
From 1:
ATS = 0.1546 if n=32, 0.0884 if n=1/32.
Another equation I found for calculating thread shear area is:
2. Ath = 0.5∏dpLe
source: http://www.engineersedge.com/thread_strength/thread_bolt_stress_area_iso.htm
Where:
dp = pitch diameter of thread = 0.3547"
Le = length of thread engagement = 0.15"
From 2:
Ath = 0.0836. This isn't far off of the second answer from 1.
A third option from Engineer's Edge is an online calculator:
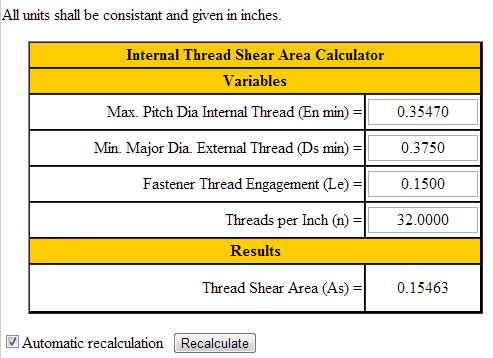
This matches the first answer of 0.1546in2 from 1.
OK, if I take those two numbers and put them into:
3. F = SUATS
Where:
SU = ultimate shear strength of the nut or bolt materials. In this case, the nut is the weaker material. The nuts is to be made of ABS, SU = 3625psi, taken from tensile strength * 0.5.
ATS = 0.1546in2 and 0.0884in2 taken from 1.
∴ if ATS = 0.1546, then F = 560.425lb
if ATS = 0.0884, then F = 320.45lb
Using this, then calculate torque required using:
4. Tin = F((P/2∏) + ((μtrt)/cosβ) + μnrn)
Where:
Tin = torque applied to the fastener
F = preload created in the fastener
P = thread pitch in inches = 1/32
μt = the coefficient of friction between the nut and bolt threads = 0.15
rt = the effective contact radius of the threads = 0.3547 = dp (I am unsure of this being correct)
β = half of the angle of the thread = 30°
μn = the coefficient of friction between the face of the nut and the upper surface of the joint (not relevant) = 0
rn = the effective radius of contact between the nut and joint surface (not relevant) = 0
But there is another equation, and completely different method, here.
I believe this link is calculating when the shank will fail, as the equation for F uses σT as opposed to SU.
Using 4:
If F = 560.425lb, Tin = 37.21in-lb
If F = 320.45lb, Tin = 21.28in-lb
The second number, 21.28in-lb seems to be within the range of what the FUTEK bolt torque calculator suggested. However, there are so many variables I am not certain of within these equations that I need to know more and if I am going wrong somewhere.
Please can anyone offer some advice, if not a definitive answer?
Many thanks.
A. The maximum force (as preload) required to reach the yield point of the nut material.
B. The torque required to achieve the above.
The thread is 3/8-32 UNEF. The male part is either nickel plated brass or zinc, and the female part is injection moulded ABS.
The length of engagement is 0.15".
I have found a few equations, but different sources list different methods. What I have also found is nobody cares how much torque it requires to strip a thread, as the more common goal is to calculate how much preload is required to yield the shank.
First, I put the numbers into the FUTEK bolt torque calculator:
17in-lb sounds like a reasonable figure for maximum torque and near what I'd expect.
It would be nice if FUTEK displayed the equations they derived their answers from, but they don't.
So, here are some of the methods and equations I have found:
1. ATS = ∏nLeDsmin((1/2n) + 0.57735(Dsmin - Emax))
Where:
ATS = Shear area of root of nut threads (in2)
n = threads per inch = 32
Le = length of thread engagement = 0.15"
Dsmin = minimum OD of bolt threads = 0.375"
Enmax = maximum PD of nut = 0.3547"*
*Calculated using:
Enmax = dp = D - 0.64592p
Where p = 1/32
I confirmed the pitch diameter of 0.3547" from this chart.
From 1:
ATS = 0.1546 if n=32, 0.0884 if n=1/32.
Another equation I found for calculating thread shear area is:
2. Ath = 0.5∏dpLe
source: http://www.engineersedge.com/thread_strength/thread_bolt_stress_area_iso.htm
Where:
dp = pitch diameter of thread = 0.3547"
Le = length of thread engagement = 0.15"
From 2:
Ath = 0.0836. This isn't far off of the second answer from 1.
A third option from Engineer's Edge is an online calculator:
This matches the first answer of 0.1546in2 from 1.
OK, if I take those two numbers and put them into:
3. F = SUATS
Where:
SU = ultimate shear strength of the nut or bolt materials. In this case, the nut is the weaker material. The nuts is to be made of ABS, SU = 3625psi, taken from tensile strength * 0.5.
ATS = 0.1546in2 and 0.0884in2 taken from 1.
∴ if ATS = 0.1546, then F = 560.425lb
if ATS = 0.0884, then F = 320.45lb
Using this, then calculate torque required using:
4. Tin = F((P/2∏) + ((μtrt)/cosβ) + μnrn)
Where:
Tin = torque applied to the fastener
F = preload created in the fastener
P = thread pitch in inches = 1/32
μt = the coefficient of friction between the nut and bolt threads = 0.15
rt = the effective contact radius of the threads = 0.3547 = dp (I am unsure of this being correct)
β = half of the angle of the thread = 30°
μn = the coefficient of friction between the face of the nut and the upper surface of the joint (not relevant) = 0
rn = the effective radius of contact between the nut and joint surface (not relevant) = 0
But there is another equation, and completely different method, here.
I believe this link is calculating when the shank will fail, as the equation for F uses σT as opposed to SU.
Using 4:
If F = 560.425lb, Tin = 37.21in-lb
If F = 320.45lb, Tin = 21.28in-lb
The second number, 21.28in-lb seems to be within the range of what the FUTEK bolt torque calculator suggested. However, there are so many variables I am not certain of within these equations that I need to know more and if I am going wrong somewhere.
Please can anyone offer some advice, if not a definitive answer?
Many thanks.
Last edited: