Second fundamental theorem of calculus viewed as a transform?

In summary, the second fundamental theorem of calculus involves transforming a function f(t) into a function of f(x) through the use of the dummy variable t. This transformation can be seen as a valid way to view the theorem, which states that two transforms (DF and If) are inverse and not obvious from the picture.
  • #1
vanmaiden
102
1
You see this picture of the second fundamental theorem of calculus
32e174d296c019dcd366191d117c3385.png
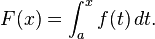and you are taught in high school / early college calculus that the t is a dummy variable. However, couldn't you view this as some sort of transform? You convert a function f(t) into a function of f(x). Is this a valid way to view this fundamental theorem of calculus?

Thanks,

Vanmaiden
 

Attachments

  • Second fundamental theorem of calculus.png
    Second fundamental theorem of calculus.png
    843 bytes · Views: 469
Physics news on Phys.org
  • #2
Yes the theorem is that two transforms are inverse
[tex]DF=\lim{h\rightarrow 0} \frac{F(x+h)-F(x)}{h}[/tex]
[tex]If=\int_a^x f(t) dt[/tex]

The fundamental theorem is that
IDF=F
and
DIf=f
which is not obvious
 

FAQ: Second fundamental theorem of calculus viewed as a transform?

What is the Second Fundamental Theorem of Calculus?

The Second Fundamental Theorem of Calculus is a mathematical theorem that relates the integral of a function to its antiderivative. It states that if f(x) is a continuous function on the interval [a, b], and F(x) is the antiderivative of f(x), then the definite integral of f(x) from a to b is equal to F(b) - F(a).

How is the Second Fundamental Theorem of Calculus viewed as a transform?

The Second Fundamental Theorem of Calculus can be viewed as a transform because it transforms the problem of calculating a definite integral into the simpler problem of finding the antiderivative of a function.

What is the relationship between the First and Second Fundamental Theorems of Calculus?

The First and Second Fundamental Theorems of Calculus are closely related. The First Fundamental Theorem states that the derivative of the integral of a function is equal to the original function. The Second Fundamental Theorem, on the other hand, states that the integral of a function is equal to its antiderivative. Together, these two theorems form the basis of integral calculus.

What are the applications of the Second Fundamental Theorem of Calculus?

The Second Fundamental Theorem of Calculus has many applications in mathematics and science. It is used to calculate areas and volumes, to solve differential equations, and to model real-world phenomena such as population growth and fluid dynamics.

Are there any limitations to the Second Fundamental Theorem of Calculus?

While the Second Fundamental Theorem of Calculus is a powerful tool in calculus, it does have some limitations. It can only be applied to continuous functions, and the antiderivative must be expressible in terms of elementary functions. In some cases, the antiderivative may not be easily calculable, making the theorem difficult to apply.

Similar threads

B Question about the fundamental theorem of calculus
Replies
2
Views
1K
B A proof of the fundamental theorem of calculus
Replies
6
Views
2K
I Questions about the fundamental thoerem of calculus
Replies
10
Views
2K
MHB Fundamental theorem of calculus and more....
Replies
9
Views
2K
I Visual interpretation of Fundamental Theorem of Calculus
Replies
5
Views
2K
The first fundamental theorem of calculus
Replies
2
Views
1K
Why is ##g## differentiable only on ##(a,b)## and not on ##[a,b]##?
Replies
12
Views
2K
First Fundamental Theorem of Calculus
Replies
15
Views
2K
Antiderivatives and the fundamental theorem
Replies
7
Views
2K
Fundamental theorem of calculus for double integral
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top