Hill
- 735
- 575
- Homework Statement
- Write down the next-order diagrams. Check the answer using Green's function method.
- Relevant Equations
- Equation of motion: ##\Box h - \lambda h^2 -J =0##
It has been shown in the text that ##h_0 = \frac 1 {\Box} J## with the diagram

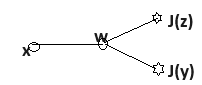
and that ##h_1 = \lambda \frac 1 {\Box} (h_0 h_0) = \lambda \frac 1 {\Box} [( \frac 1 {\Box} J)( \frac 1 {\Box}J)]## with the diagram
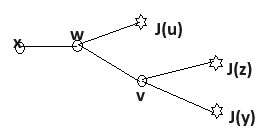
I was not sure if the next order diagram is
or rather
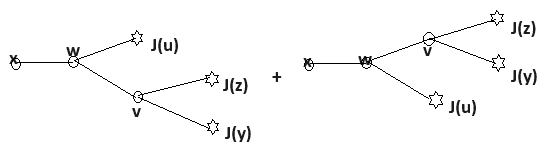
Thus, I substitute ##h=h_0+h_1+h_2## in the equation of motion and calculate to the ##\mathcal O(\lambda^2)##. I get ##\Box h_2 = 2 \lambda h_0 h_1##.
I understand that the factor 2 means that the last diagram above is correct.
Is it so?
and that ##h_1 = \lambda \frac 1 {\Box} (h_0 h_0) = \lambda \frac 1 {\Box} [( \frac 1 {\Box} J)( \frac 1 {\Box}J)]## with the diagram
I was not sure if the next order diagram is
or rather
Thus, I substitute ##h=h_0+h_1+h_2## in the equation of motion and calculate to the ##\mathcal O(\lambda^2)##. I get ##\Box h_2 = 2 \lambda h_0 h_1##.
I understand that the factor 2 means that the last diagram above is correct.
Is it so?