- #1
LSMOG
- 62
- 0
I tried to convert the second order ordinary differential equation to a system of first order differential equations and to write it in a matrix form. I took it from the book by LM Hocking on (Optimal control). What did I do wrong in this attachment because mine
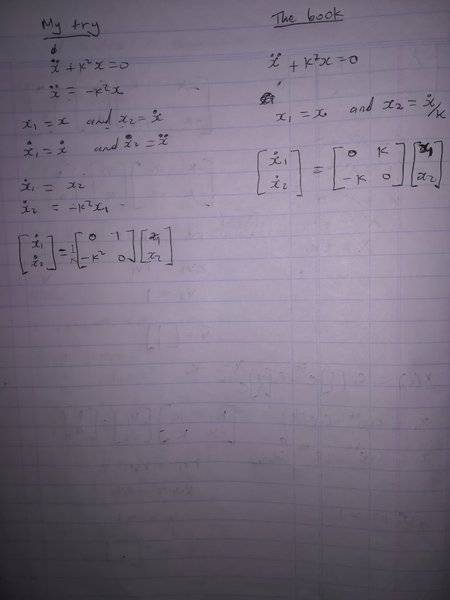 differs from the book?. I've attached both the book solution and mine. Thanks.
differs from the book?. I've attached both the book solution and mine. Thanks.
