Second Quantization in QFT

[sophiatev]

TL;DR Summary

Confused by the derivation of the Hamiltonian in Quantum Field Theory and the Standard Model by Schwartz when he discusses second quantization of the electromagnetic field

In Quantum Field Theory and the Standard Model by Schwartz, he defines the Hamiltonian for the free electromagnetic field as

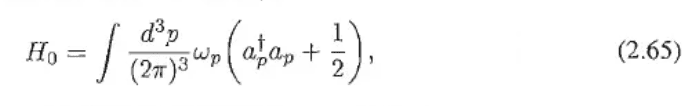
(page 20, here's a link to the book). This follows (in my understanding) from the fact that the amplitude of the field at a given point in space oscillates as a simple harmonic oscillator, i.e. the field can be written as the following equation

with the $(d^2_t + p * p)a_p(t) = 0$ condition having exactly the form of the equation for a harmonic oscillator. My question is two-fold:

1. Where did the $1/(2\pi \hbar)$ (Schwartz sets $\hbar = c = 1$, so I'm assuming, perhaps erroneously, that $1/(2\pi) = 1/(2\pi \hbar)$) factor in the denominator of equation 2.65 come from? If it's from equation 2.59, then where did it come from in 2.59? It seems similar to the situation we have for phase-space integrals, where we have to discretize phase-space by a factor of $\hbar$ to account for the position-momentum uncertainty principle, but I'm not sure. Could also be related to Fourier series, since that's what equation 2.59 apparently is.

2. In the case of the quantum harmonic oscillator, it makes sense to interpret $V = 1/2m \omega^2 x^2$ and $K = -\frac{\hbar^2}{2m}\frac{d^2}{dx^2}$ since the oscillating particle actually has mass and therefore a potential/kinetic energy associated with it in its oscillation. Using these expressions, we can derive the Hamiltonian $H = K + P = \hbar \omega(a_+ a_- + 1/2)$ for raising and lowering operators $a_+$ and $a_-$. But the field associated with equation 2.59 is explicitly massless, so I'm not sure why we are associating a kinetic/potential energy with it. I see that the amplitude has the same equation of motion as a harmonic oscillator, but I'm not sure why that means it's valid to then associate the same Hamiltonian with that amplitude. And I know that we associate energy with fields (i.e. $u = \frac{1}{2}(\epsilon_0E^2 + 1/\mu_0 B^2)$ in E&M), I just don't see why it's valid here. And why are we even taking the "energy of the amplitude's motion" (if it is valid to refer to it that way) as the energy associated with the field as a whole? That seems to be the implication here, but I'm not sure why it's justified. I seem to have a fundamental misunderstanding about what the Hamiltonian represents in "second quantization". Any help is greatly appreciated.

 

[Demystifier]

1. It comes from
$$\int\frac{dp}{2\pi}e^{ipx}=\delta(x)$$

2. To understand the meaning of Hamiltonian in second quantization, don't think of it as second quantization. Think of it as field theory. For instance, think of massles Klein-Gordon equation $\Box\phi(x)=0$ as a Newton equation for fields
$$\mu \ddot\phi(t,{\bf x})=F[\phi]$$
where the force is given by
$$F[\phi]=\mu\nabla^2\phi(t,{\bf x})$$
Here $\mu$ is an arbitrary "mass" parameter that cancels out in the Newton equation and is written just for the sake of writing the equation in the form of Newton equation. As you know from classical mechanics of particles, there exists a Hamiltonian such that the Newton equation is equivalent to Hamilton equations. The Hamiltonian for field theory is a Hamiltonian for which the corresponding Hamilton equations are equivalent to the Newton equation for fields above. Since the equation of motion does not really depend on the "mass" parameter $\mu$, it's unphysical so one can take for $\mu$ any value one wants. In actual equations in the literature you will never see $\mu$ explicitly, which can be interpreted as the choice $\mu=1$. A more correct interpretation is that mass is not essential at all to define the Hamiltonian; what is essential is that you have some equation of motion and the Hamiltonian is there to reproduce those equations of motion.

 

[vanhees71]

To "derive" a Hamiltonian, i.e., to "invent" a theory you need of course some concept, which is not necessarily mathematically rigorous. At the end you have to derive the observable consequences from your model and test it by an experiment.

For a quantum field theory (which is what was called "2nd quantization" in the early days of modern quantum mechanics though it's just another way to formulate quantum theory of indistinguishable particles in a convenient way, i.e., having a formalism which takes into acount the complete symmetry (bosons) or antisymmetry (fermions) of the states under exchange of identical particles in a convenient way) the most simple heuristics is "canonical quantization" of a classical field theory.

Photons (i.e., the quantizing of the em. field) is a bit tough for a forum posting, because you have to deal with the obstacles of gauge invariance. So let's do it for the most simple case, i.e., a scalar (Klein-Gordon) field and free uncharged particles.

For "canonical quantization" you first need a Lagrangian to define an action function functional for the classical theory. You start with a Lagrange density for the (in this case real) Klein-Gordon field. It reads
$$\mathcal{L}=\frac{1}{2} (\partial_{\mu} \phi) (\partial^{\mu} \phi)-\frac{m^2}{2} \phi^2.$$
Then the action reads
$$S=\int \mathrm{d}^4 x \mathcal{L}.$$
The equations of motion follow from Hamilton's action principle, i.e., the field equation of motion follows from making $S$ stationary under variations of $\phi$. The result are the "Euler-Lagrange equations",
$$\partial_{\mu} \frac{\partial \mathcal{L}}{\partial (\partial_{\mu} \phi)}=\frac{\partial \mathcal{L}}{\partial \phi}.$$
In how case you indeed get the Klein-Gordon equation for a free particle
$$(\Box+m^2) \phi=0$$
with $\Box=\partial_{\mu} \partial^{\mu}=\partial_0^2-\Delta$.
So the Lagrangian is the one we want.

To do quantum theory we need a formulation in terms of Hamilton's formulation with Poisson brackets. For our purposes it is sufficient to define the "canonial field momentum",
$$\Pi=\frac{\partial \mathcal{L}}{\partial \dot{\phi}}.$$
Now the canonical quantization comes as a heuristical (handwaving) concept. One just makes the field an operator (in this case a self-adjoint operator, because the classical field is assumed to be real) and interprets as an observable (or more generally a building block to express observables) in the Heisenberg picture of the time evolution and imposes the "canonical equal-time commutation relations" (in analogy of the Heisenberg algebra for position and (canonical) momentum in standard quantum mechanics in "1st quantization"):
$$[\hat{\phi}(t,\vec{x}),\hat{\phi}(t,\vec{y})]=0, \quad [\hat{\Pi}(t,\vec{x}),\hat{\Pi}(t,\vec{y})]=0, \quad [\hat{\phi}(t,\vec{x}),\hat{\Pi}(t,\vec{x})]=\delta^{(3)}(\vec{x}-\vec{y}).$$
Finally to get the complete quantum-theoretical system you need the Hamiltonian, but that's also given by the usual formalism. For the classical theory it's
$$H=\int \mathrm{d}^3 x \underbrace{[\dot{\phi}(x) \Pi(x)-\mathcal{L}]}_{\mathcal{H}}.$$
Using the above Lagrangian you get
$$\mathcal{H}=\frac{1}{2} \Pi^2+\frac{1}{2} (\vec{\nabla} \phi)^2+\frac{m^2}{2} \phi^2.$$
The Hamiltonian in the quantized theory follows from this by simply making $\phi \rightarrow \hat{\phi}$ and $\Pi \rightarrow \hat{\Pi}$, courageously ignoring possible operator-ordering problems. Though there seem to be none in this case, there indeed are some, as we'll see in a moment.

You can show that the usual equations for the field operators and canonical field momenta indeed lead back to the Klein-Gordon equation for $\hat{\phi}$, and this you can solve in the usual way via a Fourier transformation. In this context it's more convenient to use the relativistic normalization convention as in Schwartz's book given in Eq. (2.75):
$$\hat{\phi}(x)=\int_{\mathbb{R}^3} \mathrm{d}^3 \vec{p} \frac{1}{(2 \pi)^3 \sqrt{2 E_{\vec{p}}}} [\hat{a}(\vec{p}) \exp(-\mathrm{i} p \cdot x) + \hat{a}^{\dagger}(\vec{p}) \exp(\mathrm{i} p \cdot x)]_{p^0=E_{\vec{p}}}$$
with $E_{\vec{p}}=\sqrt{m^2+\vec{p}^2}>0$.

It also follows that the commutation relations for the annihilation and creation operators are
$$[\hat{a}(\vec{p}),\hat{a}(\vec{p}')]=0, \quad [\hat{a}(\vec{x}),\hat{a}^{\dagger}(\vec{p}')]=(2 \pi)^3 \delta^{(3)}(\vec{p}-\vec{p}').$$
Expressing the Hamiltonian in terms of the field operators the trouble with the operator-ordering problem pops up:
$$\hat{H}=\int_{\mathbb{R}^3} \mathrm{d}^3 p \frac{1}{(2 \pi)^3} \frac{1}{2} E_{\vec{p}} [\hat{a}^{\dagger}(\vec{p}) \hat{a}(\vec{p}) + \hat{a}(\vec{p}) \hat{a}^{\dagger}(\vec{p})].$$
This leads to a diverging ground-state energy. The "cure" for this is to subtract an infinite constant $\propto \hat{1}$ and use the well-defined "normal-ordered" Hamiltonian
$$:\hat{H}:=\int_{\mathbb{R}^3} \mathrm{d}^3 p \frac{1}{(2 \pi)^3} E_{\vec{p}} \hat{a}^{\dagger}(\vec{p}) \hat{a}(\vec{p}).$$
You can show that the normal-ordered expressions for the momentum, and four-angular momentum lead to the usual expressions and indeed generate spatial translations and proper orthochronous Lorentz transformations. Together with $\hat{H}$, which generates time translations, this leads to an irreducible unitary representation of the proper orthochronous Poincare group, acting on the field operators as the corresponding Poincare transformations on the classical field (i.e., in a "local" way).

In addition, using the Bose commutation relations, leads to the boundedness of $\hat{H}$ from below, i.e., all energy eigenvalues are $E \geq 0$ and the microcausality property, according to which the commutators of local observables (particularly the Hamilton density) vanish when the space-time arguments of these operators are space-like separated.

Though the canonical formalism is not manifestly covariant this shows that you get a local relativistic QFT and, when adding local interaction terms to the Lagrangian/Hamiltonian, a Poincare covariant unitary S-matrix obeying the cluster decomposition principle.

The same formalism works for the Dirac field. You only have to use fermionic equal-time anti-commutators when quantizing the fields. In this case you also have to write down the field operators in the mode decomposition with a annihilation operator $\hat{a}(\vec{p},\sigma)$ and a creation operator $\hat{b}^{\dagger}(\vec{p},\sigma)$, where $\hat{b} \neq \hat{a}$ in this case, because the Dirac field operators are not self-adjoint, leading to the prediction of the existence of anti-particles with the same mass but an opposite charge, where the charge is the Noether charge of the global symmetry under multiplication of the field operator with an arbitrary phase factor. One can show that only then you get all the nice properties (boundedness of $\hat{H}$, i.e., stability of the ground state and micro-causality of the local observable operators) needed for a local relativistic QFT.

 

[sophiatev]

To "derive" a Hamiltonian, i.e., to "invent" a theory you need of course some concept, which is not necessarily mathematically rigorous. At the end you have to derive the observable consequences from your model and test it by an experiment.

For a quantum field theory (which is what was called "2nd quantization" in the early days of modern quantum mechanics though it's just another way to formulate quantum theory of indistinguishable particles in a convenient way, i.e., having a formalism which takes into acount the complete symmetry (bosons) or antisymmetry (fermions) of the states under exchange of identical particles in a convenient way) the most simple heuristics is "canonical quantization" of a classical field theory.

Photons (i.e., the quantizing of the em. field) is a bit tough for a forum posting, because you have to deal with the obstacles of gauge invariance. So let's do it for the most simple case, i.e., a scalar (Klein-Gordon) field and free uncharged particles.

For "canonical quantization" you first need a Lagrangian to define an action function functional for the classical theory. You start with a Lagrange density for the (in this case real) Klein-Gordon field. It reads
$$\mathcal{L}=\frac{1}{2} (\partial_{\mu} \phi) (\partial^{\mu} \phi)-\frac{m^2}{2} \phi^2.$$
Then the action reads
$$S=\int \mathrm{d}^4 x \mathcal{L}.$$
The equations of motion follow from Hamilton's action principle, i.e., the field equation of motion follows from making $S$ stationary under variations of $\phi$. The result are the "Euler-Lagrange equations",
$$\partial_{\mu} \frac{\partial \mathcal{L}}{\partial (\partial_{\mu} \phi)}=\frac{\partial \mathcal{L}}{\partial \phi}.$$
In how case you indeed get the Klein-Gordon equation for a free particle
$$(\Box+m^2) \phi=0$$
with $\Box=\partial_{\mu} \partial^{\mu}=\partial_0^2-\Delta$.
So the Lagrangian is the one we want.

To do quantum theory we need a formulation in terms of Hamilton's formulation with Poisson brackets. For our purposes it is sufficient to define the "canonial field momentum",
$$\Pi=\frac{\partial \mathcal{L}}{\partial \dot{\phi}}.$$
Now the canonical quantization comes as a heuristical (handwaving) concept. One just makes the field an operator (in this case a self-adjoint operator, because the classical field is assumed to be real) and interprets as an observable (or more generally a building block to express observables) in the Heisenberg picture of the time evolution and imposes the "canonical equal-time commutation relations" (in analogy of the Heisenberg algebra for position and (canonical) momentum in standard quantum mechanics in "1st quantization"):
$$[\hat{\phi}(t,\vec{x}),\hat{\phi}(t,\vec{y})]=0, \quad [\hat{\Pi}(t,\vec{x}),\hat{\Pi}(t,\vec{y})]=0, \quad [\hat{\phi}(t,\vec{x}),\hat{\Pi}(t,\vec{x})]=\delta^{(3)}(\vec{x}-\vec{y}).$$
Finally to get the complete quantum-theoretical system you need the Hamiltonian, but that's also given by the usual formalism. For the classical theory it's
$$H=\int \mathrm{d}^3 x \underbrace{[\dot{\phi}(x) \Pi(x)-\mathcal{L}]}_{\mathcal{H}}.$$
Using the above Lagrangian you get
$$\mathcal{H}=\frac{1}{2} \Pi^2+\frac{1}{2} (\vec{\nabla} \phi)^2+\frac{m^2}{2} \phi^2.$$
The Hamiltonian in the quantized theory follows from this by simply making $\phi \rightarrow \hat{\phi}$ and $\Pi \rightarrow \hat{\Pi}$, courageously ignoring possible operator-ordering problems. Though there seem to be none in this case, there indeed are some, as we'll see in a moment.

You can show that the usual equations for the field operators and canonical field momenta indeed lead back to the Klein-Gordon equation for $\hat{\phi}$, and this you can solve in the usual way via a Fourier transformation. In this context it's more convenient to use the relativistic normalization convention as in Schwartz's book given in Eq. (2.75):
$$\hat{\phi}(x)=\int_{\mathbb{R}^3} \mathrm{d}^3 \vec{p} \frac{1}{(2 \pi)^3 \sqrt{2 E_{\vec{p}}}} [\hat{a}(\vec{p}) \exp(-\mathrm{i} p \cdot x) + \hat{a}^{\dagger}(\vec{p}) \exp(\mathrm{i} p \cdot x)]_{p^0=E_{\vec{p}}}$$
with $E_{\vec{p}}=\sqrt{m^2+\vec{p}^2}>0$.

It also follows that the commutation relations for the annihilation and creation operators are
$$[\hat{a}(\vec{p}),\hat{a}(\vec{p}')]=0, \quad [\hat{a}(\vec{x}),\hat{a}^{\dagger}(\vec{p}')]=(2 \pi)^3 \delta^{(3)}(\vec{p}-\vec{p}').$$
Expressing the Hamiltonian in terms of the field operators the trouble with the operator-ordering problem pops up:
$$\hat{H}=\int_{\mathbb{R}^3} \mathrm{d}^3 p \frac{1}{(2 \pi)^3} \frac{1}{2} E_{\vec{p}} [\hat{a}^{\dagger}(\vec{p}) \hat{a}(\vec{p}) + \hat{a}(\vec{p}) \hat{a}^{\dagger}(\vec{p})].$$
This leads to a diverging ground-state energy. The "cure" for this is to subtract an infinite constant $\propto \hat{1}$ and use the well-defined "normal-ordered" Hamiltonian
$$:\hat{H}:=\int_{\mathbb{R}^3} \mathrm{d}^3 p \frac{1}{(2 \pi)^3} E_{\vec{p}} \hat{a}^{\dagger}(\vec{p}) \hat{a}(\vec{p}).$$
You can show that the normal-ordered expressions for the momentum, and four-angular momentum lead to the usual expressions and indeed generate spatial translations and proper orthochronous Lorentz transformations. Together with $\hat{H}$, which generates time translations, this leads to an irreducible unitary representation of the proper orthochronous Poincare group, acting on the field operators as the corresponding Poincare transformations on the classical field (i.e., in a "local" way).

In addition, using the Bose commutation relations, leads to the boundedness of $\hat{H}$ from below, i.e., all energy eigenvalues are $E \geq 0$ and the microcausality property, according to which the commutators of local observables (particularly the Hamilton density) vanish when the space-time arguments of these operators are space-like separated.

Though the canonical formalism is not manifestly covariant this shows that you get a local relativistic QFT and, when adding local interaction terms to the Lagrangian/Hamiltonian, a Poincare covariant unitary S-matrix obeying the cluster decomposition principle.

The same formalism works for the Dirac field. You only have to use fermionic equal-time anti-commutators when quantizing the fields. In this case you also have to write down the field operators in the mode decomposition with a annihilation operator $\hat{a}(\vec{p},\sigma)$ and a creation operator $\hat{b}^{\dagger}(\vec{p},\sigma)$, where $\hat{b} \neq \hat{a}$ in this case, because the Dirac field operators are not self-adjoint, leading to the prediction of the existence of anti-particles with the same mass but an opposite charge, where the charge is the Noether charge of the global symmetry under multiplication of the field operator with an arbitrary phase factor. One can show that only then you get all the nice properties (boundedness of $\hat{H}$, i.e., stability of the ground state and micro-causality of the local observable operators) needed for a local relativistic QFT.

Turns out I had some reading to do to be able to understand your reasoning, but now that I'm caught up, that made sense, thank you . One thing I wanted to clarify - when you impose the canonical commutation relations on $\hat{\phi}$ and $\hat{\Pi}$, you do so "axiomatically", correct? Imposing these doesn't follow from anything else? The reason I ask is because I remember in my undergraduate quantum mechanics courses we proved the commutation relations for $\hat{x}$ and $\hat{p}$ based on their form, whereas in this case we seem to be imposing them without any "justification".

 

[vanhees71]

The "canonical commutation relations" are just heuristic guess work. As I said, as a theoretical physicist you often play around with some vague mathematical ideas and if you are lucky it works.

"Canonical quantization" just works for sufficiently simple observables. Already in quantum mechanics ("1st quantization") it works for the Heisenberg algebra for $\hat{x}$ and $\hat{p}$. The idea behind it is to turn the Poisson brackets of classical Hamiltonian mechanics to commutators of self-adjoint operators (times $1/\text{i}$ to make it consistent).

This is only, because this observable algebra is simple enough. It already fails for the quantization of the rigid body ("spinning top"). The correct quantization must be done using the correct Lie algebra of the rotation group (see Landau Lifshitz vol. 3 or Kleinert's book on path integrals).