Seeding a Solar System Simulation

[Bane1998]

I've coded a physics simulator that simulates the solar system. Essentially it just calculates gravity between bodies and attracts them together, the most basic simulation.

But obviously just feeding in positions for the sun and the planets will just have them all fall into directly each other. So I need to seed them in their proper orbits with the correct mass, position, and velocity. With those parameters I expect the orbits to behave correctly if my gravity calculations are correct.

For now I just place each planet at a random position on a plane with the sun at the center, at a distance equal to the orbital semimajor axis for that planet. I give it the correct mass, and I calculate a circular orbit speed via:

// v = sqrt(((m2 * m2) * g) / ((m1 + m2) * r)
// where:
// v == orbital velocity
// m1 == orbiter mass
// m2 == orbited mass
// g == gravitational constant
// r == distance between objects

Sending it off at that speed in a direction perpendicular to it's vector from the sun.

I've tested this with the Earth and a space-shuttle sized object, and I see a steady almost perfectly circular orbit. It's barely elliptical I assume due to rounding errors of floating points and negligible effects of gravity applied to the Earth and what not. But it's close enough I'd call it circular, so I've verified my basic simulation works.

Now however I want to seed it with more realistic elliptical orbits. I've done a lot more digging on the subject and the closest I can find to a solution is combining:

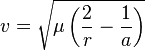
from http://en.wikipedia.org/wiki/Orbital_mechanics

and

μ = Gm1 + Gm2

from http://en.wikipedia.org/wiki/Standard_gravitational_parameter

into:

// v = sqrt(((g * m1) + (g * m2)) * ((2 / r) - (1 / a)))
// where:
// v == orbital velocity
// g == gravitational constant
// m1 == orbiter mass
// m2 == orbited mass
// r == distance between objects
// a == length of semi-major axis

But not only does it not quite seem to work for anything but perfectly circular orbits, I don't see how it possibly COULD work, given it seems to be missing inputs, like the eccentricity or the semi-minor axis.

By the way, I don't want to just cheat and look up the current position and speed of the planets because I am rolling this into a game where I want to randomly generate planetary systems with sensical input parameters(random reasonable ranges) about the orbits.

So, I am obviously not understanding how to do this. Any help would be appreciated. I know if I had a better understanding of the basics and ellipses I could probably derive a solution, but I'm a little bit over my head perhaps. There seems to be lots of information about finding the position on an ellipse given the angle, but I can't figure out how to turn this into a velocity like I need.

Sorry for the long and probably overly-verbose post. I hate even asking, I usually just spend days crawling wikipedia and struggling through it eventually coming up with an answer and then working out backwards why it works, but that doesn't seem to be working in this case for me.

(Was just looking around, this might be the wrong place for this actually. I apologize if so, not sure if this qualifies as a homework type question or not. I'll happily delete and repost in a more appropriate forum if needed.)

 

[Filip Larsen]

Extending directly from what you already have, maybe you can use the angle between the radius and velocity vector, $\phi$, found on [1] as

$$\sin\phi = \sqrt{\frac{a^2(1-e^2)}{r(2a-r)}}$$

However, to turn this into a position and velocity vector for 2D simulation you also need to find the true anomaly and the argument of perihelion, and for a 3D simulation you also need inclination and longitude of ascending note (see [2]). I guess for random data you can just make these elements random within some relevant interval.

For a general overview of orbital mechanics you may find [3] useful.[1] Orbital Motion, A.E. Roy, Adam Hilger, 1988.
[2] http://en.wikipedia.org/wiki/Argument_of_periapsis
[3] http://www.braeunig.us/space/orbmech.htm

 

[Bane1998]

So my second equation I did not understand:

from http://en.wikipedia.org/wiki/Orbital_mechanics

and

μ = Gm1 + Gm2

from http://en.wikipedia.org/wiki/Standard_gravitational_parameter

into:

// v = sqrt(((g * m1) + (g * m2)) * ((2 / r) - (1 / a)))
// where:
// v == orbital velocity
// g == gravitational constant
// m1 == orbiter mass
// m2 == orbited mass
// r == distance between objects
// a == length of semi-major axis

But not only does it not quite seem to work for anything but perfectly circular orbits, I don't see how it possibly COULD work, given it seems to be missing inputs, like the eccentricity or the semi-minor axis.

since it seems like the semi major axis is not enough information. For example if I'm in an elliptical orbit around a body at the center of the ellipse, and I'm at a distance equal to the semi major, then the speed should just depend on the eccentricity, which doesn't seem to be captured in the inputs at all.

I think my fatal mistake was 'in an elliptical orbit around a body at the center of the ellipse.' Since that is actually an invalid state unless it's a circle. Which is why the output of that function is the speed of the circular orbit when the distance is equal to the semi-major axis, and not ambiguous with any elliptical orbits. Which is an interesting relationship to 'feel' in my brain. Speed of a circular orbit == Speed of an elliptical orbit when at a distance equal to the semi-major axis. Is that true?

Also, my initial assumption about how to calculate an orbit was that the direction vector is always a right angle to the relative position vector, but this is untrue for an ellipse (I think), so I need more than just speed.

If nothing else, posting here helps me think through a problem 'out loud' and forces me to try to use correct terminology as much as I can. :)

Thank you for that link.

P.S. Just re-read what you posted and it looks like you might have just given me the other piece of information I just realized I need, the direction vector. Which makes you a whole lot smarter than me, figuring out what I need before I realize I need it. :)

 

[Filip Larsen]

I think my fatal mistake was 'in an elliptical orbit around a body at the center of the ellipse.'

Yes, the other mass lies at one of the focus points of the ellipse. See fig. 4.2 in my previous reference [3].

Speed of a circular orbit == Speed of an elliptical orbit when at a distance equal to the semi-major axis. Is that true?

Yes. For a non-circular orbit the speed is the same at two points in the orbit, but direction will be either above the "horizontal" or below it (like in fig. 4.8 on [3]).

Also, my initial assumption about how to calculate an orbit was that the direction vector is always a right angle to the relative position vector, but this is untrue for an ellipse (I think), so I need more than just speed.

You can find a simple version of most of what you need again in [3] in the section "Position in an Elliptical Orbit" (right after fig. 4.8) using the equations (4.32) to (4.39) and some simple trigonometry. In two dimensions you can get the Cartesian (x,y) coordinates of the position of the orbiting body as

(1) $$r_x = r \cos(\nu+\omega)$$

and

(2) $$r_y = r \sin(\nu+\omega)$$

where $\omega$ is the argument of perihelion and $\nu$ is the true anomaly and assuming the central mass is placed in the center of your coordinate system. The velocity vector can be found as

(3) $$v_x = -v \sin(\nu+\omega-\phi)$$

and

(4) $$v_y = v \cos(\nu+\omega-\phi)$$

where $\phi$ is the flight path angle as shown in fig. 4.8 in [3].

By the way, equation (1) to (4) is valid for a prograde orbit, that is, an orbit where the orbiting mass orbits counter-clockwise. For a retrograde orbit that orbits clockwise you should use $\nu$ with reverse sign it in equations (1) and (2), and $\omega$ with reverse sign in equations (3) and (4).

 

[Bane1998]

Grr, I wrote a more elaborate post but it timed out my login and threw away my post when it redirected me from the login prompt. That's super-lame. *rages at crappy forum software*

So, since I don't want to re-write it all, I'll jump to the point.

Am I correct that I cannot start with a 0-1 uniform time and get a correct position/vector? Eccentric and True Anomalies are not uniform, and there's no exact solution to go from a Mean Anomaly to the either of the other two, from what I can tell.

I see an approximation formula for conversion to true or eccentric, but just an approximation. How much error does this have? Is it any better than just treating eccentric or true anomalies as uniform even though they aren't? How much better?

Why isn't there an exact solution? Why may be a dangerous question well above my education level, but I'm curious. Doesn't this make it impossible to exactly model the solar system at any time in the future? How do programs like Universe Sandbox pull it off?

If I randomly generate the true or eccentric anomalies there will be a bias towards the slow side of the orbit, yes? If I randomly generate mean anomalies and use the approximation formula will I get a closer to correct result?

 

[Filip Larsen]

Grr, I wrote a more elaborate post but it timed out my login and threw away my post when it redirected me from the login prompt. That's super-lame. *rages at crappy forum software*

I often make a copy of my post before submitting; just pressing ctrl-A and ctrl-C and I have a copy to paste with ctrl-V if I have to start over.

Am I correct that I cannot start with a 0-1 uniform time and get a correct position/vector? Eccentric and True Anomalies are not uniform, and there's no exact solution to go from a Mean Anomaly to the either of the other two, from what I can tell.

Yes.

I see an approximation formula for conversion to true or eccentric, but just an approximation. How much error does this have? Is it any better than just treating eccentric or true anomalies as uniform even though they aren't? How much better?

It is just an approximation, but there are iterative methods that will allow you to find the eccentric and true anomaly with whatever precision you want. Please have a look at https://www.physicsforums.com/showpost.php?p=3242748&postcount=7

Regarding the precision needed for the true anomaly it relates to what you use it for. If every new position of a planet is calculated again from time and its orbital element, then you only need enough precision in true anomaly to server your need for precision for that one position since next time you calculate you "start over" anyway. If on the other hand you use the position as input to a numerical integration then you would need much better precision in true anomaly since any errors are "accumulated" when integrating.

To give you a sense of what precision in true anomaly you may need, you can relate the error in true anomaly, $\delta\nu$ in radians, with the error in position along the orbit, $\delta s$, as

$$\delta s = r \delta\nu$$

where $r$ is the orbital radius of the body.

Why isn't there an exact solution? Why may be a dangerous question well above my education level, but I'm curious.

It relates to how various functions are defined in mathematics. You may want to search for the term "Transcendental Equation".

Doesn't this make it impossible to exactly model the solar system at any time in the future?

In itself, no. As I mentioned above, there is no limit to how accurate you can determine the true anomaly from mean anomaly using numerical methods. However, since we only know the (measured) state of the object in the solar system with a certain precision and the interaction between the bodies have potential for chaotic motion there is a limit to how long into the future we can accurately calculate the orbit of the bodies. For major bodies I seem to remember that our current model able to cover around the order of 50 millions years or so.

How do programs like Universe Sandbox pull it off?

I assume it just calculate the position and velocity of each object (which can be done fairly accurately using extended tables and calculations) and then integrate from that. I do not know the innards of this program, but I assume it is more focused on showing the user some "interesting" dynamics than being able to accurately integrated trajectories far into the future.

If I randomly generate the true or eccentric anomalies there will be a bias towards the slow side of the orbit, yes? If I randomly generate mean anomalies and use the approximation formula will I get a closer to correct result?

There is a difference between these two, sure, but I guess it really depends on what you consider a "correct result".

 

[Bane1998]

Thank you for all your help! I actually have it working in 3D now, that's just my flattened view for debugging. I can calculate position, speed, directional vector up to a given accuracy for the sattelite. In the image above the directional vector is the speed scaled by a factor of 100 so I can visualize it.

Was quite a challenge for me. :)

 

[Bane1998]

It's important to give back, so for any other non-math-genius programmers, here is the code, highly commented. I won't bother you to help me any further, but if yer bored/interested in glancing at the comments, maybe you can tell me if my terminology or description of what's going on is incorrect. I don' think it's buggy, as it seems to work.

The vector math is just my naive implementation once I have the 'hard' math handled. I'm sure there's a more direct way to get the vectors in 3d, but this works. :)

    public class Orbit
    {
        // To mathematically describe an orbit one must define six quantities, called orbital elements.
        // The first two describe the shape of the ellipse
        // The next three are angles to place the ellipse correctly around the body
        // The last parameter is the time at which the orbiter was at a given poin in the orbit

        // Semi-Major Axis is half the length of the Major Axis of the Ellipse, which is the length
        // from one far side of an ellipse to the other (meters)
        public double SemiMajorAxis;

        // Eccentricity is the distance between the foci divided by the length of the major axis and
        // is a number between zero and less than one. An eccentricity of zero indicates a circle. If
        // it is 1 or greater it's not a closed loop (meters)
        public double Eccentricity;

        // Inclination is the angle (radians of course) between the orbit's plane and the reference plane,
        // which is usually the equator plane of the object being orbited, or in the case of the sun, the
        // plane on which the Earth orbits. (Earth has an inclination of 0 by definition in that case)
        public double Inclination;

        // Nodes are the points where the orbit crosses the reference plane. If it's the node that the
        // body moves up from the southern side of the plane, then it's the ascending node, otherwise it's
        // the descending node. The Longitude of the Ascending Node is the angle counter-clockwise from a
        // reference vector
        public double LongitudeOfAscendingNode;

        // Periapsis is the point at which the orbit is closest to the body being orbited. The Argument of
        // Periapsis is angle between the ascending node and the periapsis
        public double ArgumentOfPeriapsis;

        // Time of Periapsis Passage is the time at which the planet was at periapsis (closest)
        public double TimeOfPeriapsisPassage;

        // Along with the orbital parameters, we need the two bodies in orbit, for when Mass is
        // part fo the orbit equations
        public Body Orbiter;
        public Body Orbiting;

        public double GetOrbitalPeriod()
        {
            // T = (2 * pi * sqrt((a * a * a) / ((G * m1) + (G * m2))))
            //   where:
            //     T = orbital period
            //     a = semi-major axis
            //     G = gravitational constant
            //     m1 = mass of body 1
            //     m2 = mass of body 2

            double a = this.SemiMajorAxis;
            double G = MathHelper2.GravitationalConstant;
            double m1 = this.Orbiter.Mass;
            double m2 = this.Orbiting.Mass;
            return (2 * Math.PI * Math.Sqrt((a * a * a) / ((G * m1) + (G * m2))));
        }

        public double GetMeanMotion()
        {
            // n = sqrt((G * (m1 + m2)) / (a * a * a))
            //   where:
            //     n = mean motion
            //     G = gravitational constant
            //     m1 = mass of body 1
            //     m2 = mass of body 2
            //     a = semi-major axis
            // -OR-
            // n = (2 * pi) / P
            //   where:
            //     n = mean motion
            //     P = orbital period

            // We use the calculation without the period, since the period is actually
            // just derivitive from existing values we already have (it's not in the
            // definition of our orbit)
            double G = MathHelper2.GravitationalConstant;
            double m1 = this.Orbiter.Mass;
            double m2 = this.Orbiting.Mass;
            double a = this.SemiMajorAxis;

            return Math.Sqrt((G * (m1 + m2)) / (a * a * a));
        }

        public double GetCurrentMeanAnomaly(double time)
        {
            // M = (n * t)
            //   where:
            //     n = mean motion
            //     t = time
            return (this.GetMeanMotion() * time);
        }

        public double GetCurrentTrueAnomaly(double time, double accuracy)
        {
            // v = (2 * arctan(sqrt((1 + e) / (1 - e)) * tan(E / 2)))
            //   where:
            //     v = true anomaly
            //     E = eccentric anomaly
            //     e = eccentricity

            double E = GetCurrentEccentricAnomaly(time, accuracy);
            double e = this.Eccentricity;
            return (2.0 * Math.Atan(Math.Sqrt((1.0 + e) / (1.0 - e)) * Math.Tan(E / 2.0)));
        }

        public double GetCurrentEccentricAnomaly(double time, double accuracy)
        {
            // This is not exactly computable, however, we can approximate it up to
            // an accuracy, by progressively getting more correct. The reason you
            // cannot directly comput it is because E is on both sides of the equality,
            // so we keep evaluating it until it evaluates close enough. In other terms,
            // it's self-referencing.

            // E = M + e * sin(E)
            //   where:
            //     E = eccentric anomaly
            //     M = mean anomaly
            //     e = eccentricity

            double M = this.GetCurrentMeanAnomaly(time);
            double e = this.Eccentricity;

            // We either start with the Mean Anomaly directly
            double E = M;

            // Or if we are highly eccentric we can start with Pi
            if (e > 0.8)
                E = Math.PI;

            // Let's start iterating
            while (true)
            {
                // Calculate a new E using the last E
                double newE = M + e * Math.Sin(E);

                // If the new E and the last E are close enough,
                // then we can be done
                if (Math.Abs(newE - E) < accuracy)
                {
                    E = newE;
                    break;
                }

                E = newE;
            }

            return E;
        }

        public double GetCurrentDistance(double time, double accuracy)
        {
            // r = (a * (1.0 - (e * cos(E))))
            //   where:
            //     r = distance to orbit from orbited body
            //     a = semi-major axis
            //     e = orbital eccentricity
            //     E = eccentric anomaly

            double a = this.SemiMajorAxis;
            double e = this.Eccentricity;
            double E = this.GetCurrentEccentricAnomaly(time, accuracy);

            return (a * (1.0 - (e * Math.Cos(E))));
        }

        public double GetCurrentAngle(double time, double accuracy)
        {
            // Current Angle is just the true anomaly
            return this.GetCurrentTrueAnomaly(time, accuracy);
        }

        public double GetCurrentFlightPathAngle(double time, double accuracy, double trueAnomaly = double.NaN)
        {
            // o = flight path angle
            //   where:
            //     o = arctan((e * sin(v)) / (1 + (e * cos(v))))
            //     e = orbital eccentricity
            //     v = true anomaly

            double e = this.Eccentricity;
            double v = trueAnomaly;
            if (double.IsNaN(v))
                v = this.GetCurrentTrueAnomaly(time, accuracy);

            return Math.Atan((e * Math.Sin(v)) / (1 + (e * Math.Cos(v))));
        }

        public double GetCurrentSpeed(double time, double accuracy)
        {
            // s = (sqrt(G * (m1 + m2) * a * (1 - (e * e))) / (r * cos(o)))
            //   where:
            //     s = speed
            //     G = gravitational constant
            //     m1 = mass of body 1
            //     m2 = mass of body 2
            //     a = semi-major axis
            //     e = orbital eccentricity
            //     r = distance to orbit from orbited body
            //     o = flight path angle
            
            double G = MathHelper2.GravitationalConstant;
            double m1 = this.Orbiter.Mass;
            double m2 = this.Orbiting.Mass;
            double a = this.SemiMajorAxis;
            double e = this.Eccentricity;
            double r = this.GetCurrentDistance(time, accuracy);
            double v = this.GetCurrentTrueAnomaly(time, accuracy);
            double o = GetCurrentFlightPathAngle(time, accuracy, v);

            return (Math.Sqrt(G * (m1 + m2) * a * (1 - (e * e))) / (r * Math.Cos(o)));
        }

        public Vector3d GetCurrentPosition(double time, double accuracy)
        {
            Vector3d ascendingNode = Vector3d.Transform(this.Orbiting.ReferenceVector, Quaterniond.CreateFromAxisAngle(this.Orbiting.UpVector, this.LongitudeOfAscendingNode));
            Vector3d unInclinedPeriapsis = Vector3d.Transform(ascendingNode, Quaterniond.CreateFromAxisAngle(this.Orbiting.UpVector, this.ArgumentOfPeriapsis));
            Vector3d periapsis = Vector3d.Transform(unInclinedPeriapsis, Quaterniond.CreateFromAxisAngle(ascendingNode, this.Inclination));
            Vector3d orbitalUp = Vector3d.Transform(this.Orbiting.UpVector, Quaterniond.CreateFromAxisAngle(ascendingNode, this.Inclination));

            double angle = GetCurrentAngle(time, accuracy);
            return Vector3d.Transform(periapsis, Quaterniond.CreateFromAxisAngle(orbitalUp, angle)) * GetCurrentDistance(time, accuracy);
        }

        public Vector3d GetCurrentVelocity(double time, double accuracy)
        {
            Vector3d ascendingNode = Vector3d.Transform(this.Orbiting.ReferenceVector, Quaterniond.CreateFromAxisAngle(this.Orbiting.UpVector, this.LongitudeOfAscendingNode));
            Vector3d unInclinedPeriapsis = Vector3d.Transform(ascendingNode, Quaterniond.CreateFromAxisAngle(this.Orbiting.UpVector, this.ArgumentOfPeriapsis));
            Vector3d periapsis = Vector3d.Transform(unInclinedPeriapsis, Quaterniond.CreateFromAxisAngle(ascendingNode, this.Inclination));
            Vector3d orbitalUp = Vector3d.Transform(this.Orbiting.UpVector, Quaterniond.CreateFromAxisAngle(ascendingNode, this.Inclination));

            double angle = GetCurrentAngle(time, accuracy) - GetCurrentFlightPathAngle(time, accuracy);
            Vector3d curPos = Vector3d.Transform(periapsis, Quaterniond.CreateFromAxisAngle(orbitalUp, angle));
            Vector3d direction = Vector3d.Cross(curPos, orbitalUp);

            return direction * GetCurrentSpeed(time, accuracy);
        }
    }

    public class Body
    {
        public double Mass;

        // Axial Tilt is just the angle between (0,0,1) and (1,0,0) transformed by this orientation
        public Quaterniond Orientation = Quaterniond.Identity;

        // Used by orbits to get the plane of reference and a reference vector. These do not
        // change since the body doesn't change orientation (we are ignoring wobble, or will
        // apply wobble as some function after the static orientation)
        public Vector3d UpVector { get { return Vector3d.Transform(Vector3d.UnitZ, this.Orientation); } }
        public Vector3d ReferenceVector { get { return Vector3d.Transform(Vector3d.UnitX, this.Orientation); } }
    }

 

[Filip Larsen]

For what its worth, I've looked through your code as if it was a kind of code critique for a college and while I have found nothing major I do have a few comments. Let's take the general comments first:

• Consider including code comments about that all angels are in radians, all masses are in kg, and all distances are in meter unless otherwise noted. Consider mentioning that time parameters are to be understood time intervals indicating seconds since periapsis passage.
• If this code has to have high performance there is plenty of opportunity for optimizing the calculations, especially with caching already calculated values. For instance, there is no point in recalculating mean motion unless some of the involved parameters in the calculation has changed. In C# a manually coded property setters can be used instead of just simple fields to detect changes in parameters as a part of a caching mechanism.

I have the following comments for specific parts of your code (line numbers refer to the line number the the code you posted above):

• 14: Eccentricity is a dimensionless number (not meters).
• 17: Negative inclination is often used to model retrograde orbits. I am not able to see if this works for your code.
• 26,30: Note, that the value of longitude of ascending node is undefined when the inclination is zero. Often, one uses the longitude of periapsis (defined as the sum of the longitude of ascending node and argument of periapsis) instead of argument of periapsis, and then substract longitude of ascending note where argument of perigee is needed.
• 33: Orbital elements are often given where time of periapsis passage, t_p, is replaced with mean eccentricity at epoch, M₀, and time of epoch, t₀, so that mean anomaly then can be calculated as M = M₀ + n(t-t₀) instead of M = n(t-t_p). By the way, it seems TimeOfPeriapsisPassage is not used in this code snippet.
• 54: Consider storing G*M for each body instead of just M. Calculating G*M is fine when you use random data for M, but in real life the value G*M is often known much more precisely than M due to G being only known with relatively low number of significant digits. Also, consider calling GetMeanMotion in part of the expression to avoid "code duplication" with GetMeanMotion.
• 105: Consider using a Newton-iteration to solve Keplers equation as it often converges much faster that the simple iteration.
• 130-146: Consider if it is necessary to guard against infinite looping. Consider using a do-while loop instead, e.g.
  do { 
    double newE = ...; 
    E = newE; 
  } while (Math.Abs(newE-E) > accuracy);
• 171: Using NaN as special value is a bit obscure. Consider making two methods with different parameter list instead, e.g method
  public double GetCurrentFlightPathAngle(double time, double accuracy) { 
    return GetCurrentFlightPathAngle(time, accuracy, GetCurrentTrueAnomaly(time,accuracy));
  }
  public double GetCurrentFlightPathAngle(double time, double accuracy, double trueAnomaly) { 
    return ...;
  }
• 209: Consider using the relation v² = G(m₁+m₂)(2/r-1/a) instead.
• 212-236: Not reviewed.

You can of course use or ignore these comments at your own discretion.

 

[Bane1998]

Hey, back again!

Do these equations take into account the two body problem?

I'm using mass for both the orbiter and the orbited in my physics simulation, however I just don't apply any force to the orbited object to keep it still. But comparing my simulation to these orbit calculations, I see increasing error for increasing mass of the orbiter.

Allowing force to be applied to orbited object does not seem to help. Are these orbit calculations only valid assuming the orbiter has no mass?

 

[Bane1998]

Interesting. If I remove the mass of the orbiter from the orbital equations, there's no error.

The orbital equations should not include the mass of the orbiter? The mass of the orbiting body doesn't affect the orbit? That doesn't make sense to me since calculating the gravity force in the physics simulation uses both masses.

Or is that only true because I don't apply gravitational force to the orbited body (I keep it pinned to the origin).

 

[Filip Larsen]

When two masses orbit each other they do so "around" the common center of mass, called the barycenter [1], which lies the distance

$$r_2 = r \frac{m_1}{m_1+m_2}$$

from the center of m₂ towards m₁, or equivalently, the distance

$$r_1 = r \frac{m_2}{m_1+m_2}$$

from the center of m₁ towards m₂, where r is the distance between the two centers at any given time (the distance you calculate in your code).

Using the combined mass, e.g. G(m₁+m₂), is the correct mass to use in a two-body problem. However, you can plot the position of the smaller mass, say m₁, using its distance to the barycenter (which corresponds to fixed point in your plot) by plotting r₁ instead of r.

Does this help?


[1] http://en.wikipedia.org/wiki/Center_of_mass#Barycenter_in_astrophysics_and_astronomy

 

[mikeph]

I'm using mass for both the orbiter and the orbited in my physics simulation, however I just don't apply any force to the orbited object to keep it still. But comparing my simulation to these orbit calculations, I see increasing error for increasing mass of the orbiter.

It's not the two body problem if the sun is held fixed. Moulton (1984) is a very good book detailing the mathematics of the two body problem (online derivations are generally rubbish or fragmented) which should give a good introduction.

I didn't read the entire code (and don't understand that language anyway), what are the basics of your solver? Is it iterative? something like v(k) = v(k-1) + acceleration*t, x(k) = x(k-1) + v(k)*t?

 

[Bane1998]

When two masses orbit each other they do so "around" the common center of mass, called the barycenter [1], which lies the distance

$$r_2 = r \frac{m_1}{m_1+m_2}$$

from the center of m₂ towards m₁, or equivalently, the distance

$$r_1 = r \frac{m_2}{m_1+m_2}$$

from the center of m₁ towards m₂, where r is the distance between the two centers at any given time (the distance you calculate in your code).

Using the combined mass, e.g. G(m₁+m₂), is the correct mass to use in a two-body problem. However, you can plot the position of the smaller mass, say m₁, using its distance to the barycenter (which corresponds to fixed point in your plot) by plotting r₁ instead of r.

Does this help?


[1] http://en.wikipedia.org/wiki/Center_of_mass#Barycenter_in_astrophysics_and_astronomy

I see, so the error I'm seeing between my physics simulation and my orbit calculation is that I'm setting the moon in orbit around the center of the earth.

My physics sim correctly computes the orbit around the barycenter because that just falls out of the gravity force computations, but the orbital calculation is incorrect (and different from the physics sim) because it's assuming around the center of the earth, which is fine with no mass on the moon because the barycenter is the same as the center of the Earth in that case.

I'm glad I understand what's going on now, but now I wonder if it's worth solving, I think at this point I'm just getting pedantic. Since this is just the background for a game, forcing the barycenter to be the center of the more massive object might just be how I keep it. Though, it's fun learning all this. :)

 

[Bane1998]

It's not the two body problem if the sun is held fixed. Moulton (1984) is a very good book detailing the mathematics of the two body problem (online derivations are generally rubbish or fragmented) which should give a good introduction.

I didn't read the entire code (and don't understand that language anyway), what are the basics of your solver? Is it iterative? something like v(k) = v(k-1) + acceleration*t, x(k) = x(k-1) + v(k)*t?

Er, I don't know anything about solvers, I'm a bit of a dunce. :)

The code I pasted was just the result of me learning how to calculate a position and velocity for a body in orbit based on a time input function.

For context, essentially what I'm doing is simulating the solar system (more specifically, any randomly generated solar system) for a video game. The first thing I did was implement a really naive physics 'engine' that just keeps a set of objects with position and momentum vectors, responding to force vectors, one of the automatic force vectors being the force of gravity. It just ticks in fixed steps of arbitrary resolution, so i don't think that's really a solver, if solver means what I think it means.

However, keeping the solar system 'ticking' when players are not in the solar system would be a waste of resources, so when there are no live players in that system, I will shut the physics down. Which means I need to be able to solve (I'm assuming this is the solver term yer using) where all the orbital bodies SHOULD be when a player returns at an arbitrary time in the future. And in fact, in the end it might not even be worth it to put the planets into the physics sim, I could just use the solver in realtime, too.

But since I have both a simulation, and an orbital solver already implemented now, I'm using them to check each other. A body in orbit should be in the same position both according to the running physics simulation, and the orbital solver.

What my last post was trying to say is that I'm seeing the two answers diverge, and I'm reasonably sure after reading Filip's response that it's because my orbital solver assumes the center of the orbited body is the point around which you orbit, which is actually not true (and evident with the physics sim).

I should also probably say gravity sim, not physics sim.

Not sure if that answers your question, because I don't understand your question. But I tried. :)

P.S. I know due to floating point errors getting compounded the gravity sim will become increasingly incorrect over long periods, which is another reason I might just use the solver in realtime, too.

 

[Bane1998]

When two masses orbit each other they do so "around" the common center of mass, called the barycenter [1], which lies the distance

$$r_2 = r \frac{m_1}{m_1+m_2}$$

from the center of m₂ towards m₁, or equivalently, the distance

$$r_1 = r \frac{m_2}{m_1+m_2}$$

from the center of m₁ towards m₂, where r is the distance between the two centers at any given time (the distance you calculate in your code).

Using the combined mass, e.g. G(m₁+m₂), is the correct mass to use in a two-body problem. However, you can plot the position of the smaller mass, say m₁, using its distance to the barycenter (which corresponds to fixed point in your plot) by plotting r₁ instead of r.

Does this help?


[1] http://en.wikipedia.org/wiki/Center_of_mass#Barycenter_in_astrophysics_and_astronomy

The barycenter is only a fixed point if I allow both objects to move. In my simulation I only allow the moon to move, and the Earth remains pinned at the origin, so in that case, the barycenter is moving in a perfect circle from the center of the Earth towards the moon, yes?

So for my orbit calculation I need to first calculate the barycenter. If I'm correct that the barycenter forms a perfect circle in this case, the barycenter distance is constant. However, the direction of the barycenter from the Earth is more complicated. It has to be in the direction of the moon, which actually depends on where the barycenter is in the first place, so I'm left with a self referential problem, no?

Maybe it would be easier to redefine my system to be barycenters of systems orbiting other systems, so my barycenter is always at the origin in it's own local simulation. Then I keep my existing orbit calculations as a single mass problem, applying them to both objects around the barycenter.

I feel like the more correct I try to be, the deeper down the rabbit hole I go into things I have to learn. :)

 

[Neandethal00]

Extending directly from what you already have, maybe you can use the angle between the radius and velocity vector, $\phi$, found on [1] as

$$\sin\phi = \sqrt{\frac{a^2(1-e^2)}{r(2a-r)}}$$

However, to turn this into a position and velocity vector for 2D simulation you also need to find the true anomaly and the argument of perihelion, and for a 3D simulation you also need inclination and longitude of ascending note (see [2]). I guess for random data you can just make these elements random within some relevant interval.

@Bane1998
The above formula is probably the best to start with. I once used this formula for simulation of a few planets, with ONE BIG problem, I'll explain later. This is how I used the equation.

a) Solve the equation for 'r'. r is the radial distance of ,say, Earth from one focus of the ellipse.

b) compute 'x' and 'y' component of 'r'. This 'x' and 'y' are the coordinates of the center of Earth (planet). Draw the planet at this point.

c) You have to get from online the accurate values of 'e' and and semi-major axis 'a' of each planet.

d) Note, you'll be incrementing the angle from 0 to 360 degrees in simulation.

Now the Problem:The graphics work beautifully but against Kepler 3rd law. When the planet is closer to the sun, its velocity is slower, when the planet is farther from the sun, its velocity is faster. IIRC, Kepler's law says exactly the opposite.

Anyone here knows how to correct the simulation for velocity?

 

[mikeph]

The reason I ask is because in a true simulation (everything can move, everything subject to Newton's law of gravity), simple iterative schemes diverge very fast, because the system is chaotic (mathematical term, meaning it's very difficult to predict). Decent iterative schemes do exist though (ranging in complexity, depending on how long you want the system to remain accurate).

You could probably get a reasonable estimate by just prescribing the positions of each planet as a function of time in a simple way, neglecting the gravitational force between planets, and fixing the sun at the centre. In that way it would also be very easy to find the positions at some later date without having to do all the calculations up to that point. You'd just need a timer to run in the background, then plug that time into the equations. Depends how accurate you want to be. I don't know what gravity sim is but I presume if it is accurate, it is also complicated.

regarding barycentres: if you hold a planet fixed, the barycentre is indeed moving in a circle, like you imagine. However this has some subtle implications. Because you fix your coordinates so that an accelerating body is always at the origin, your coordinates are accelerating. A mass which has no forces on it will appear, in your coordinates, to be accelerating by itself. Newton's 2nd law isn't broken, but you need to be aware that this coordinate system will create "pseudo forces" that don't exist in reality. I suggest you put the barycentre at the centre of the coordinate system and use a fixed, not accelerating, coordinate system.

 

[Bane1998]

The reason I ask is because in a true simulation (everything can move, everything subject to Newton's law of gravity), simple iterative schemes diverge very fast, because the system is chaotic (mathematical term, meaning it's very difficult to predict). Decent iterative schemes do exist though (ranging in complexity, depending on how long you want the system to remain accurate).

You could probably get a reasonable estimate by just prescribing the positions of each planet as a function of time in a simple way, neglecting the gravitational force between planets, and fixing the sun at the centre. In that way it would also be very easy to find the positions at some later date without having to do all the calculations up to that point. You'd just need a timer to run in the background, then plug that time into the equations. Depends how accurate you want to be. I don't know what gravity sim is but I presume if it is accurate, it is also complicated.

regarding barycentres: if you hold a planet fixed, the barycentre is indeed moving in a circle, like you imagine. However this has some subtle implications. Because you fix your coordinates so that an accelerating body is always at the origin, your coordinates are accelerating. A mass which has no forces on it will appear, in your coordinates, to be accelerating by itself. Newton's 2nd law isn't broken, but you need to be aware that this coordinate system will create "pseudo forces" that don't exist in reality. I suggest you put the barycentre at the centre of the coordinate system and use a fixed, not accelerating, coordinate system.

My simulation merely iterates through the objects in the simulation, applying forces to the momentum, and then acting on the momentum in fixed steps. In a simulation where everything applies gravity to everything else it becomes an O(n²) algorithm to figure out the gravity forces though, which isn't acceptable. So to get around it I only allow some objects to have the gravity well flag, and in my case that's only the main body.

The simulation is actually a series of simulations where an simulation can also be an actor, so simulations can contain other simulations. The sun is an actor in a simulation with 8 actor simulations for each of the planets. Those simulations then contain the relevant moons, etc. So I can apply gravity from only ever 1 object per simulation.

So my solar system simulation is a lot like relative transforms in a rigged mesh.

I think given this isn't for NASA or anything, I will ignore the barycenter issue, since I can't seem to make it work obviously when only the Earth applies gravity. So to make my orbit calculations work correctly in such a 'cheating' system, I need the orbiter's mass to be zero, and then it behaves in-line with the physics simulation, since even though the orbiter has mass from the point of view of the simulator, that mass does not factor into gravity since the orbiter is not a gravity well.

 

[mikeph]

I only allow some objects to have the gravity well flag, and in my case that's only the main body.

In that case, you shouldn't need to integrate at all, the exact trajectories are given by Kepler's laws of motion. Each planet will orbit the sun in an ellipse, and each moon will orbit the planet in an ellipse. You can probably find the major axes and eccentricities online.