- #1
Martian2020
- 49
- 0
- TL;DR Summary
- I want to see correct visualization of curvature of spacetime (1d space+time) in 3d for spherical object of uniform density. Kind of Minkowski diagram.
Via web search found https://www.physicsforums.com/threads/what-dimension-does-space-time-curve-in.852103/
Read it and watched two videos mentioned:
I understand we cannot perceive 5D ;-), so extrinsic visualization of maximum of 2D intrinsic curvature is possible. So time+1d space is all we can see, and it is fine for sphere due to symmetry. I know not all intrinsic can be seen as extrinsic (is my language correct here?), however I understand spacetime curvature resulting from spherical mass can be correctly embedded, right?
In linked videos general idea of object going "straight"/geodesic line in spacetime is clear. However, I would like to find/see more informative visualization of spacetime curvature of spherical body with uniform density where it is clearly seen:
1) change from "gravitational force formula" outside a sphere to "falling" inside.
2) going though center and "raising" to opposite side of the sphere; extending it to several cycles
3) like on Minkowski diagrams with c*t axis being able to visualize "steepness" of curvature for escape velosity > speed of light
I was not able to find one via web search. Best I found was thread here mentioned above.
Visualization readily available is very good, any help with making one is appreciated too!
As a side note, the below visualizations cannot obviously show full spacetime (not 5D), but maybe they are not only useful tools and analogies but also correct visualizations of something?
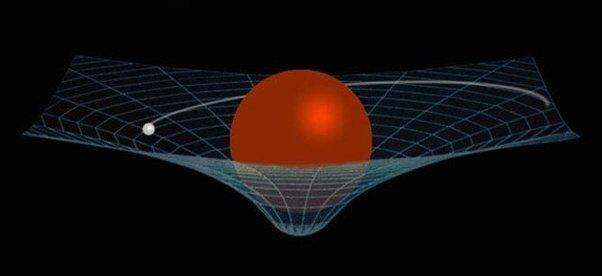
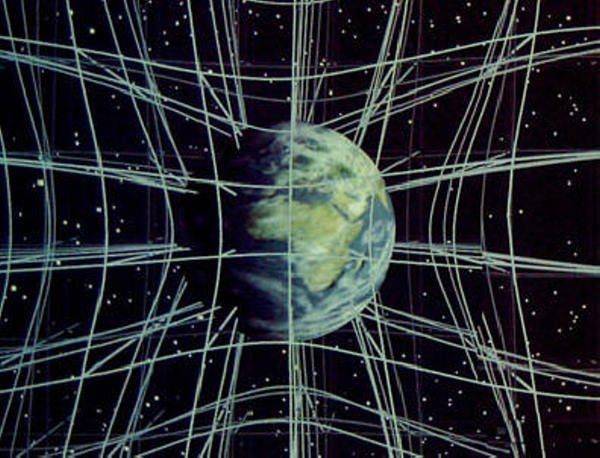
P.S. I am not sure it is "basic", I am new here.
Read it and watched two videos mentioned:
I understand we cannot perceive 5D ;-), so extrinsic visualization of maximum of 2D intrinsic curvature is possible. So time+1d space is all we can see, and it is fine for sphere due to symmetry. I know not all intrinsic can be seen as extrinsic (is my language correct here?), however I understand spacetime curvature resulting from spherical mass can be correctly embedded, right?
In linked videos general idea of object going "straight"/geodesic line in spacetime is clear. However, I would like to find/see more informative visualization of spacetime curvature of spherical body with uniform density where it is clearly seen:
1) change from "gravitational force formula" outside a sphere to "falling" inside.
2) going though center and "raising" to opposite side of the sphere; extending it to several cycles
3) like on Minkowski diagrams with c*t axis being able to visualize "steepness" of curvature for escape velosity > speed of light
I was not able to find one via web search. Best I found was thread here mentioned above.
Visualization readily available is very good, any help with making one is appreciated too!
As a side note, the below visualizations cannot obviously show full spacetime (not 5D), but maybe they are not only useful tools and analogies but also correct visualizations of something?
P.S. I am not sure it is "basic", I am new here.