warhammer
- 164
- 33
- Homework Statement
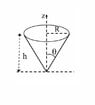
- Cone shown in figure has half angle θ, vertical height h & radius R. Its axis is along z direction. Cone is polarised along z direction with Vector P= P(o)z(zhat) where P(o) is a constant. Find surface & volume bound charge density.
- Relevant Equations
- σ(b)= P(vector) * (nhat)
ρ(b)= - ∇* P(vector)
This was a trivial question I had (which I posted here on the PF EM Forum: https://www.physicsforums.com/threads/bound-charges-polarisation-of-a-half-cone.1015308/).
As I received no response on the above link I decided to post the same as a self formulated HW problem. Below I have attached an image of the cone as well as my solution in chronological order.
I request someone to please have a look and guide me if my approach to find the Surface & Volume Bound Charges is fine or not. If it isn't, I would also request guidance on how to find it correctly .
.
As I received no response on the above link I decided to post the same as a self formulated HW problem. Below I have attached an image of the cone as well as my solution in chronological order.
I request someone to please have a look and guide me if my approach to find the Surface & Volume Bound Charges is fine or not. If it isn't, I would also request guidance on how to find it correctly