davidwinth
- 103
- 8
- Homework Statement
- Find the cable tension and the compressive force in the beam
- Relevant Equations
- Equilibrium means sum of forces equals zero
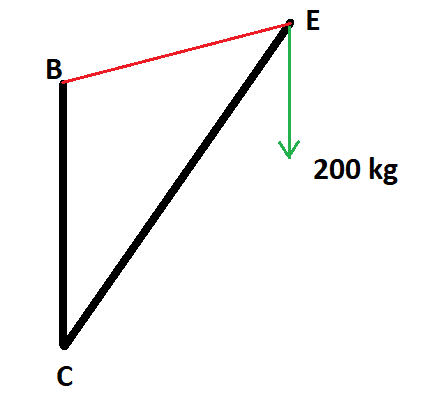
For this problem we are asked to find the tension in the cable BE and the compressive force in beam CE. We are given that ## \angle C = 40 \circ##. We are also given that CE = 10 meters and vertical BC = 6 meters.
My solution is to find BE using the law of cosines, from which I get
$$BE = \sqrt{10^2 + 6^2 - 2(6)(10)cos(40)} = 6.638875 m$$
I use the law of sines to calculate the angle E (taken as CEB) as
$$ \angle E = sin^{-1} \left ( \frac{6sin(40)}{6.638875} \right) = 35.51602 \circ$$
Now the sum of the forces in the x direction at point E is just (note the angle from the mass to E to B is 75.51602 degrees):
$$-F_{BE}sin(75.51602) + F_{CE}sin(40)=0$$
and the sum of the forces in the y direction is:
$$-F_{BE}cos(75.51602) + F_{CE}cos(40)=200*9.8$$
When I solve this I get that the cable tension is 2168.7 N and the compressive force in the beam is 3266.7 N. The textbook has a value for the cable of 2450 N and the beam of 3360 N. I am not sure why my solution is wrong.
My solution is to find BE using the law of cosines, from which I get
$$BE = \sqrt{10^2 + 6^2 - 2(6)(10)cos(40)} = 6.638875 m$$
I use the law of sines to calculate the angle E (taken as CEB) as
$$ \angle E = sin^{-1} \left ( \frac{6sin(40)}{6.638875} \right) = 35.51602 \circ$$
Now the sum of the forces in the x direction at point E is just (note the angle from the mass to E to B is 75.51602 degrees):
$$-F_{BE}sin(75.51602) + F_{CE}sin(40)=0$$
and the sum of the forces in the y direction is:
$$-F_{BE}cos(75.51602) + F_{CE}cos(40)=200*9.8$$
When I solve this I get that the cable tension is 2168.7 N and the compressive force in the beam is 3266.7 N. The textbook has a value for the cable of 2450 N and the beam of 3360 N. I am not sure why my solution is wrong.