zinn
- 1
- 0
- TL;DR Summary
- How can separation angle alone tell you about the correlation between gravitational wave signals from pulsar timing?
I’m trying to understand the Hellings and Downs curve that is being used to argue for the existence of a gravitational wave background ([NANOGrav article][1]). How can it be that the angle between two pulsars is the only variable that determines if the gravitational waves will interfere constructively (correlated) or destructively (anti-correlated). I would have imagined that distance from the observer would also be a factor.
(Image source: https://astrobites.org/2016/08/10/the-predictor-of-pulsar-timing/)
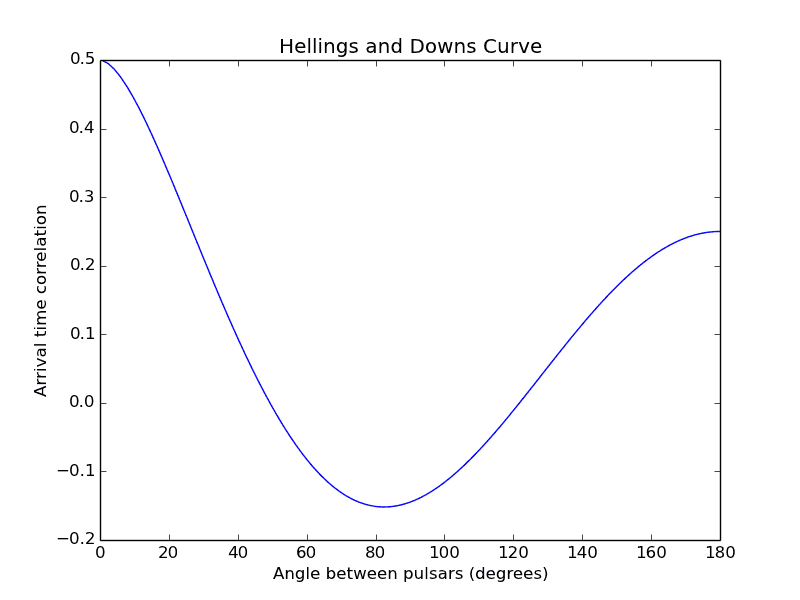
I imagine that a key part of understanding this concept would be visualising the gravitational waveforms in 3D. Should I be picturing something like this? [youtube video with gravitational wave animations][2]
[1]: https://nanograv.org/15yr/Summary/Background
[2]:
[3]: https://i.stack.imgur.com/w3DSd.png
(Image source: https://astrobites.org/2016/08/10/the-predictor-of-pulsar-timing/)
I imagine that a key part of understanding this concept would be visualising the gravitational waveforms in 3D. Should I be picturing something like this? [youtube video with gravitational wave animations][2]
[1]: https://nanograv.org/15yr/Summary/Background
[2]:
[3]: https://i.stack.imgur.com/w3DSd.png