milkism
- 118
- 15
- Homework Statement
- Need help with setting up the first part of the problem.
- Relevant Equations
- See solution.
Problem:

Solution:
When I looked at an example problem, they started writing the potential in terms of the Legendre polynomials.
The example problem:
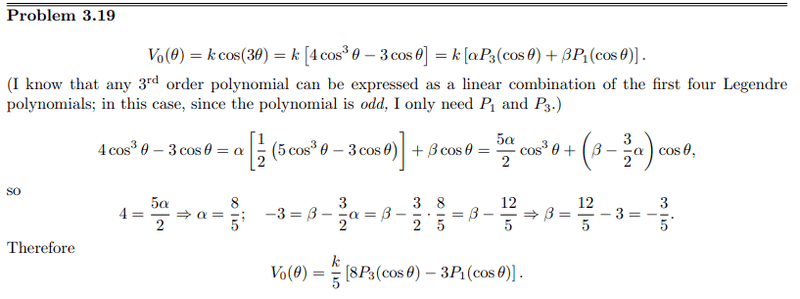
This is what I did:
$$V_0 \alpha P_2 (\cos(\theta)) \Rightarrow \frac{\alpha 3 \cos ^2 (\theta)}{2} - \frac{\alpha}{2} \Rightarrow \frac{\alpha 3}{2} - \frac{\alpha}{2}= 1 \Rightarrow \alpha = 1$$
Hence,
$$V(\theta) = V_0 P_2 (\cos(\theta)).$$
Have I done right?
Solution:
When I looked at an example problem, they started writing the potential in terms of the Legendre polynomials.
The example problem:
This is what I did:
$$V_0 \alpha P_2 (\cos(\theta)) \Rightarrow \frac{\alpha 3 \cos ^2 (\theta)}{2} - \frac{\alpha}{2} \Rightarrow \frac{\alpha 3}{2} - \frac{\alpha}{2}= 1 \Rightarrow \alpha = 1$$
Hence,
$$V(\theta) = V_0 P_2 (\cos(\theta)).$$
Have I done right?