- #1
Oppie
- 7
- 1
Hello,
I've been using "Guide to Essential Math" by S.M. Blinder from time to time to stay on top of my basic mathematics. I'm currently on the section on Bernoulli Numbers. In that section he has the following (snippet below).
Is the transition to equation 7.61 just wrong? The equation just doesn't make sense. If it is wrong, can anyone "see" what he may have had in mind? What is the "explicit" series equal to if not coth(x/2)? Thank you.
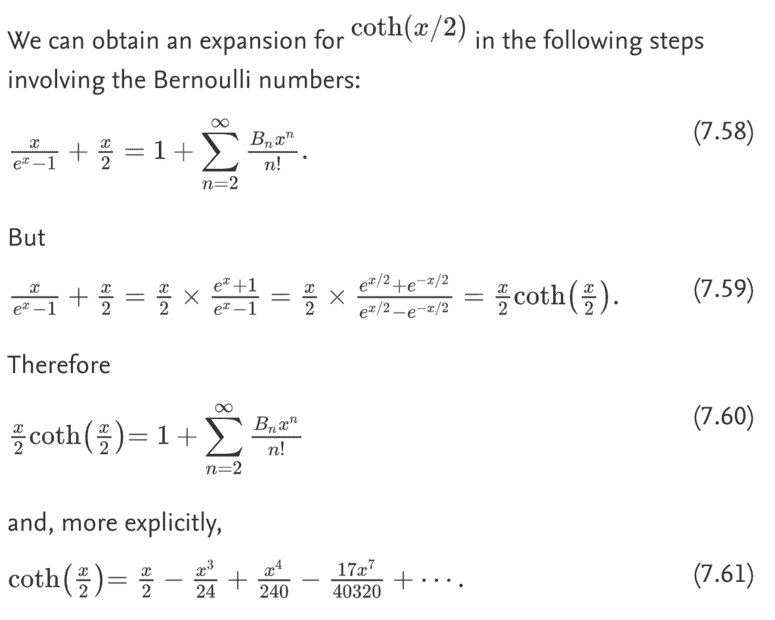
I've been using "Guide to Essential Math" by S.M. Blinder from time to time to stay on top of my basic mathematics. I'm currently on the section on Bernoulli Numbers. In that section he has the following (snippet below).
Is the transition to equation 7.61 just wrong? The equation just doesn't make sense. If it is wrong, can anyone "see" what he may have had in mind? What is the "explicit" series equal to if not coth(x/2)? Thank you.