Sets and Venn Diagrams for Real Numbers: Understanding Associative Axioms

[bergausstein]

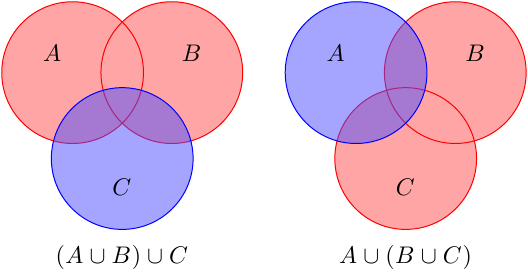
the associative axioms for the real numbers correspond to the following statements about sets: for any sets A, B, and C, we have $(A\cup B)\cup C=A\cup (B\cup C)$ and $(A\cap B)\cap C=A\cap (B\cap C)$. Illustrate each of these statements using Venn diagrams.

can you show me how to draw the first one with the union of the sets, after that I'll try to illustrate the second statement. just want to get an idea how to go about it.thanks!

 

[Evgeny.Makarov]

The task to "illustrate" is not really mathematical. It basically says, "Draw a picture that you believe would be helpful for grasping associativity of set union". But what people believe to be helpful or relevant may differ.

I would draw it like this.

The idea is that red union is done first and then one adds the blue set. In the end we are interested in the colored region, which is the same in both cases.

 

[bergausstein]

this is what i tried for the associativity of intersection.

the black circle is A, the red one is B and the blue one is C.

View attachment 1151

 

[bergausstein]

Follow up question. can we also illustrate the distributive law of intersection over union? and union over intersection? how would that look like?

 

[paulmdrdo]

yes we can.

A = BLACK
B = RED
C = BLUE
for the intersection over union i would illustrate it like this
View attachment 1152

hope this would help you illustrate the other one. :)

 

[bergausstein]

here's my try.

View attachment 1154

is this correct?

 

[caffeinemachine]

this is what i tried for the associativity of intersection.

the black circle is A, the red one is B and the blue one is C.

View attachment 1151

Good job!

- - - Updated - - -

here's my try.

View attachment 1154

is this correct?

To me this is okay. But as Evgeny.Makarov pointed out this might not be okay to someone else. Cuz he might say that 'no this does not illustrate the identity correctly' and no one can do anything about it. Don't give it too much importance. Just be sure to understand why $A\cup(B\cap C)=(A\cup B)\cap (A\cup C)$ is true. Can you show this without a diagram?

 

[bergausstein]

let say $A=\{1,2,3\}$, $B=\{4,5,6\}$, $C=\{6,7,8\}$

$A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$

$\{1,2,3\}\cup \{6\}=\{1,2,3,4,5,6\}\cap \{1,2,3,4,6,7,8\}$
$\{1,2,3,6\}=\{1,2,3,6\}$

but i know there's a more general way to show why that is true. can you show me your work? thanks! I'm weak when it comes to generalizing.

 

[caffeinemachine]

let say $A=\{1,2,3\}$, $B=\{4,5,6\}$, $C=\{6,7,8\}$

$A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$

$\{1,2,3\}\cup \{6\}=\{1,2,3,4,5,6\}\cap \{1,2,3,4,6,7,8\}$
$\{1,2,3,6\}=\{1,2,3,6\}$

but i know there's a more general way to show why that is true. can you show me your work? thanks! I'm weak when it comes to generalizing.

The general way of showing that $X=Y$ is to show that $X\subseteq Y$ and $Y\subseteq X$.

Here $X=A\cup(B\cap C)$ and $Y=(A\cap B)\cap (A\cup C)$. Let $x\in X$. Can you show that $x$ is in $Y$ too?

 

[bergausstein]

if $X\subseteq Y$ and $Y\subseteq X$ it follows that $X=Y$ and we may conclude that X and Y have precisely the same elements. we can now say that $x\in Y$ given that $x\in X$.
am i right?

and for educational purposes can anybody show me your complete work for proving the statement $A\cup(B\cap C)=(A\cup B)\cap (A\cup C)$

thanks! :)