- #1
LearninDaMath
- 295
- 0
Suppose I have a rectangle with length x and height y:
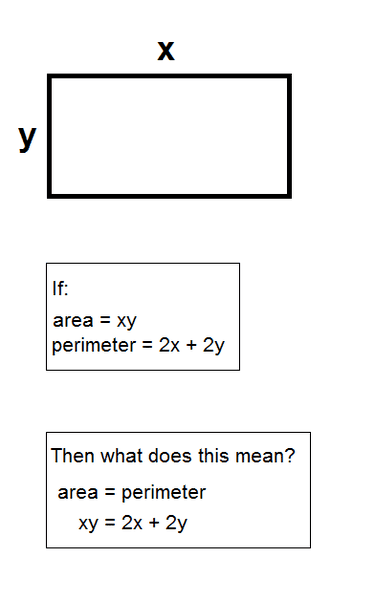 Can this ever be true? That xy = 2x+2y?
Can this ever be true? That xy = 2x+2y?
My guess would be that area of a shape can never equal the perimeter of that shape. And that would be confirmed by the fact that the equation is always false (except if both variables equal zero, but then there is no shape or perimeter which defeats the purpose of evaluating a shape's area or perimeter in the first place).
So I would say Area is apples and Perimeter is oranges. And trying to equate them doesn't work.
----------------------------------------------------------------
However, if the above conclusion is correct, how come I have an assignment that calls for the substitution of Area into Perimeter? How can mixing apples and oranges all of a sudden make sense? See following image:
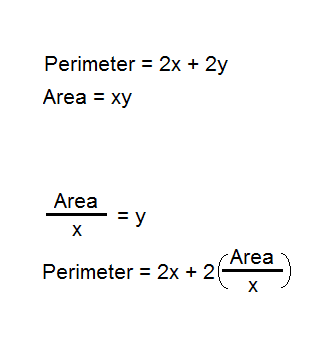
Can this be? Why so? Why does the scenario in the second image seem to conflict with the scenario in the first image?
My guess would be that area of a shape can never equal the perimeter of that shape. And that would be confirmed by the fact that the equation is always false (except if both variables equal zero, but then there is no shape or perimeter which defeats the purpose of evaluating a shape's area or perimeter in the first place).
So I would say Area is apples and Perimeter is oranges. And trying to equate them doesn't work.
----------------------------------------------------------------
However, if the above conclusion is correct, how come I have an assignment that calls for the substitution of Area into Perimeter? How can mixing apples and oranges all of a sudden make sense? See following image:
Can this be? Why so? Why does the scenario in the second image seem to conflict with the scenario in the first image?