Shallow water equations evaluation

[maistral]

Summary:: A little confusion on the momentum equation (I think).

According to Wikipedia (I know, I just need basic resources for now), the conservative SWEs are
:

If I use product rules, I am supposed to get:

For context, note that ρ is a constant and can be taken out (thus canceled out), and η(x,y) = H + h(x,y) (H is a constant).

I have no issues getting the first line. The second line however, I am facing issues. This is what I have:

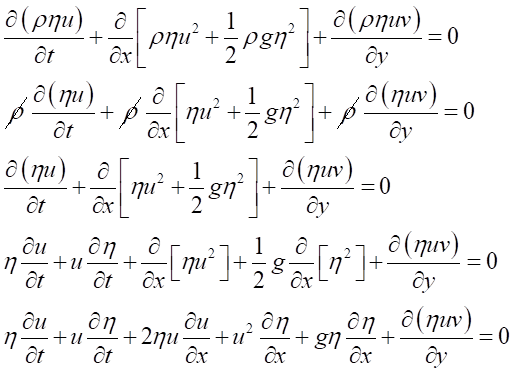
I intentionally did not distribute the derivatives with respect to y so I could see the problem more clearer. Am I missing something here with regards to the expansion of the PDE? Thanks in advance.

 

[maistral]

Just an update:

I found this paper that actually is the same 'issue' that I am facing, though they just presented it.

This paper:
https://doi.org/10.1063/5.0039545

It stated that:

I am having trouble understanding how the second equations have been made (second equation 4, to second equation 5).

 

[Haborix]

The wikipedia entry on shallow water equations doesn't make sense to me. How could you, from equations derived using momentum and mass conservation, merely expand terms and get a non-conservative set of equations. No mechanical manipulation of equations changes the underlying assumptions they were derived from.