Mayhem
- 413
- 309
- TL;DR Summary
- How to interpret the order statistic in the context of SW
Given the Shapiro-Wilk test value W:
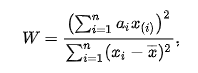
where I'm interested in the numerator. If my data is sorted in ascending order, my understanding is that $x_(i) = x_i$. Is that correct?
where I'm interested in the numerator. If my data is sorted in ascending order, my understanding is that $x_(i) = x_i$. Is that correct?
Last edited: