Shear stress at particular point in beam

[fonseh]

Homework Statement

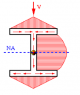
In the example , I suspect the selected A (area) is wrong... From the notes , A' is the area of top (or bottom ) portion of the member cross sectional area . But , in the example , we could see that the selected area is located to the right of the point where shear stress is calculated , is the notes wrong ?

Homework Equations

The Attempt at a Solution

[/B]
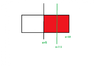
IMO , the selected A' should look like this . (refer to green part in the 3rd photo )

 

[fonseh]

Image uploaded

 

[fonseh]

Is the author wrong , or my concept is wrong ?

 

[PhanthomJay]

Is the author wrong , or my concept is wrong ?

The author is not wrong, but it is a bit confusing. Your method yields the rather low average shear stress along the entire over 200mm full width of the flange, while the solution yields the much higher shear stress in the 19.6mm flange thickness into the page. If you imagine that the the 108 mm portion of the flange was broken off from point a to the right end, and you wanted to glue it back on, you'd need a high strength glue, whereas if the full 200 mm width of flange was broken off from the top to point a and you wanted you wanted to glue it back on , you need only a low strength glue. These shear flow concepts are not explained that well in many texts , and are difficult to understand.

 

[fonseh]

The author is not wrong, but it is a bit confusing. Your method yields the rather low average shear stress along the entire over 200mm full width of the flange, while the solution yields the much higher shear stress in the 19.6mm flange thickness into the page. If you imagine that the the 108 mm portion of the flange was broken off from point a to the right end, and you wanted to glue it back on, you'd need a high strength glue, whereas if the full 200 mm width of flange was broken off from the top to point a and you wanted you wanted to glue it back on , you need only a low strength glue. These shear flow concepts are not explained that well in many texts , and are difficult to understand.

how do we know whether the shear stress yield is small or large ?

 

[PhanthomJay]

how do we know whether the shear stress yield is small or large ?

We're not talking shear yield stress we are talking actual shear stress under the given load. The solution gives 16 MPa in the flange at section a. That is higher than the shear stress averaged over the flange width which by your approach comes out to maybe on the order of 3 MPa, which is a lot lower than 16. Both stresses are well below steel yield shear stresses.

 

[fonseh]

We're not talking shear yield stress we are talking actual shear stress under the given load. The solution gives 16 MPa in the flange at section a. That is higher than the shear stress averaged over the flange width which by your approach comes out to maybe on the order of 3 MPa, which is a lot lower than 16. Both stresses are well below steel yield shear stresses.

Do you mean if follow my approach , the ans is 3 MPa, which is a lot lower than 16. Then , it's wrong ? why it is so ?

 

[PhanthomJay]

Do you mean if follow my approach , the ans is 3 MPa, which is a lot lower than 16. Then , it's wrong ? why it is so ?

The issue is that the 3 MPa shear stress in the flange calculated by your method is the average shear stress over the entire 200 mm width of the flange. Actual shear stress varies from 0 at the left end to a max at the center then back to 0 at the right end of the flange. Shear stresses are calculated at a plane, not a point. The solution gives the shear stress at a plane into the page cut by the vertical dotted line through point a. Your's gives the average shear stress at a plane cut by a horizontal line running at the bottom of the flange. As I mentioned, these are difficult concepts to grasp.

 

[fonseh]

The issue is that the 3 MPa shear stress in the flange calculated by your method is the average shear stress over the entire 200 mm width of the flange. Actual shear stress varies from 0 at the left end to a max at the center then back to 0 at the right end of the flange. Shear stresses are calculated at a plane, not a point. The solution gives the shear stress at a plane into the page cut by the vertical dotted line through point a. Your's gives the average shear stress at a plane cut by a horizontal line running at the bottom of the flange. As I mentioned, these are difficult concepts to grasp.

do you mean this ?

 

[fonseh]

The issue is that the 3 MPa shear stress in the flange calculated by your method is the average shear stress over the entire 200 mm width of the flange. Actual shear stress varies from 0 at the left end to a max at the center then back to 0 at the right end of the flange. Shear stresses are calculated at a plane, not a point. The solution gives the shear stress at a plane into the page cut by the vertical dotted line through point a. Your's gives the average shear stress at a plane cut by a horizontal line running at the bottom of the flange. As I mentioned, these are difficult concepts to grasp.

I have an example here , so the shear stress calculated is horizontal shear stress , not vertical shear stress , they are not mentioned earlier what type of stress in the question earlier ...

 

[PhanthomJay]

do you mean this ?

Yes, the peak of the triangle corresponds to the 16 MPa value . You should note that the direction of this shear stress is to the left , not vertical, and if you are familiar with the equilibrium of the 3D stress cube, the stress must also act longitudinally into the plane of the page.

 

[fonseh]

Yes, the peak of the triangle corresponds to the 16 MPa value . You should note that the direction of this shear stress is to the left , not vertical, and if you are familiar with the equilibrium of the 3D stress cube, the stress must also act longitudinally into the plane of the page.

do you mean the shear stress have the direction as shown ? p/s : the magnitude of the shear is not the true magnitude , i just want to show that the shear flow decreases as they move away from center

 

[fonseh]

I have an example here , so the shear stress calculated is horizontal shear stress , not vertical shear stress , they are not mentioned earlier what type of stress in the question earlier ...

how to determine whether it is horizontal or vertical stress acting ?

 

[PhanthomJay]

how to determine whether it is horizontal or vertical stress acting ?

Both vertical and horizontal shear stresses are acting on the flange, and each has a longitudinal shear stress associated with it.

 

[fonseh]

Both vertical and horizontal shear stresses are acting on the flange, and each has a longitudinal shear stress associated with it.

Here's from my lecturer ,
Since we want to find the horizontal shear stress(in post #1) , so we want to 'cut ' the section vertically. To cut the section vertically , so , we need vertical shear force .
Is the concept correct ?

But , in the question in post #10, it's clear that we 'cut' the section horizontally , so the shear stress acting is vertical shear stress ?

 

[PhanthomJay]

Here's from my lecturer ,
Since we want to find the horizontal shear stress(in post #1) , so we want to 'cut ' the section vertically. To cut the section vertically , so , we need vertical shear force .
Is the concept correct ?

But , in the question in post #10, it's clear that we 'cut' the section horizontally , so the shear stress acting is vertical shear stress ?

you cut the flange vertically to determine horiz and complimentary longitudinal shear stress. You cut the flange horizontally to determine vert and complimentary longitudinal shear stress.
At a vertical cut through point a , horiz and longitudinal shear is 16. At a horizontal cut through point a, vertical shear averages 3 and longitudinal shear averages 3. In post 10, there is no horizontal shear..

 

[fonseh]

At a vertical cut through point a , horiz and longitudinal shear is 16.

where does the longitidunal stress act ? in which direction ? can you draw it out ? i am confused

 

[fonseh]

In post 10, there is no horizontal shear..

why ?

 

[PhanthomJay]

Longitudinal shear stress acts into the plane of the page along the length of the beam , it is designated as q in your post on thin walls, horizontal flange shear stress accompanied by the equal magnitude longitudinal shear stress along the beam length.

When a beam is subject to vertical loads, and you want to calculate vertical shear stresses using VQ/It, Q is the area above the horizontal cut where you want to determine stresses time the distance from its centroid to the neutral axis. When you want to calculate horizontal shear stresses under the same vertical load, Q is the area to the right of the vertical cut where you want to determine stresses time the distance from its centroid to the same neutral axis. This is why you get different vertical and horizontal shear stresses in the I beam flange. But in post 10, this is a solid beam. There are no horizontal shear stresses because any area to the right of a vertical cut has its centroid located at the neutral axis, thus Q = A(y-bar) is zero because y-bar is zero. There is however a longitudinal shear stress associated with the vertical shear stress. I know you are probably still confused, because as I have mentioned, it is a difficult concept to grasp.

 

[fonseh]

There are no horizontal shear stresses because any area to the right of a vertical cut has its centroid located at the neutral axis, thus Q = A(y-bar) is zero because y-bar is zero

why ? let's say the width of the cross section is 10 , then centroid at x = 5 , so the are to the right has width of 5 , so centroid of that area that located to the right is at x= 7.5 , so ybar = 7.5-5 = 2.5 , right ? why you said ybar = 0 ?

 

[fonseh]

There is however a longitudinal shear stress associated with the vertical shear stress.

so , only vertical shear stress acting on the beam ?

 

[PhanthomJay]

why ? let's say the width of the cross section is 10 , then centroid at x = 5 , so the are to the right has width of 5 , so centroid of that area that located to the right is at x= 7.5 , so ybar = 7.5-5 = 2.5 , right ? why you said ybar = 0 ?

You are calculating ybar = 2.5 from the vertical axis, but you should be looking at ybar from the horizontal neutral axis, which is 0.

 

[PhanthomJay]

so , only vertical shear stress acting on the beam ?

vertical and complimentary longitudinal, no horizontal.

 

[fonseh]

why should the ybar is 0 when we are looking ybar from the horizontal neutral axis ? why shouldn't the ybar = 7.5 ? Same concept applied here . The

 

[fonseh]

ok , wh

You are calculating ybar = 2.5 from the vertical axis, but you should be looking at ybar from the horizontal neutral axis, which is 0.

ok , why we need to calculate ybar from horizontal neutral axis ?

 

[PhanthomJay]

why should the ybar is 0 when we are looking ybar from the horizontal neutral axis ? why shouldn't the ybar = 7.5 ? Same concept applied here . The

See post 19. Say you have a 10 by 10 cross section. Max vert shear stress is at neutral axis and using area above neut axis, Q is (10)(5)(2.5) = 125 . For max horiz shear stress , using area to the right of the vert axis of the shape, Q is (5)(10)(0) = 0.

 

[fonseh]

Longitudinal shear stress acts into the plane of the page along the length of the beam , it is designated as q in your post on thin walls, horizontal flange shear stress accompanied by the equal magnitude longitudinal shear stress along the beam length.

When a beam is subject to vertical loads, and you want to calculate vertical shear stresses using VQ/It, Q is the area above the horizontal cut where you want to determine stresses time the distance from its centroid to the neutral axis. When you want to calculate horizontal shear stresses under the same vertical load, Q is the area to the right of the vertical cut where you want to determine stresses time the distance from its centroid to the same neutral axis. This is why you get different vertical and horizontal shear stresses in the I beam flange. But in post 10, this is a solid beam. There are no horizontal shear stresses because any area to the right of a vertical cut has its centroid located at the neutral axis, thus Q = A(y-bar) is zero because y-bar is zero. There is however a longitudinal shear stress associated with the vertical shear stress. I know you are probably still confused, because as I have mentioned, it is a difficult concept to grasp.

neutral axis here means the horizontal axis ? why not vertical axis ?

 

[PhanthomJay]

neutral axis here means the horizontal axis ? why not vertical axis ?

Loading is vertically applied, so you use the horizontal neutral axis